Maths lesson – 30+ outstanding free plans for KS3 and GCSE

We’ve got everything you need for your secondary maths classroom from algebra and geometry to improving number sense and mathematical fluency…

- by Teachwire
- Classroom expertise and free resources for teachers

We’ve got maths lesson plans covering number, algebra, geometry, statistics and probability, plus lessons aimed specifically at problem-solving.
These maths lessons are from the mind of Colin Foster, a member of the maths education department at Loughborough University.
KS3 maths lesson ideas
Number
Use puzzles to explore changes in percentages

Is 50% off a better deal than 50% extra free? This percentage change KS3 lesson helps students get to grips with the issues surrounding percentage change.
Explore what makes prime numbers special

Some numbers are definitely more important than others. This prime numbers KS3 lesson plan focuses on what it is about the prime numbers that makes them special. It also looks at the idea that they are the building blocks of all the whole numbers greater than 1.
Link adding and subtracting directed numbers to electricity

Lots of learners have heard that ‘two minuses make a plus’. However, they may not apply this rule correctly or have much sense of when or why it is the case.
In this lesson, you’ll make links to the science topic of electricity to help learners understand adding and subtracting directed (positive and negative) numbers.
Explore proportions by mixing paints

In this KS3 proportion lesson, students work on a task about pink paint, which is made from a mixture of red paint and white paint.
How much red paint do you need to add to pink paint which is 60% red to turn it into pink paint which is 80% red?
Statistics and probability
Dice-rolling and lolly stick experiments

In the first of these probability KS3 lesson plans students will carry out an experiment to estimate the probability that when they throw three ordinary dice, they will show consecutive numbers.
In the second lesson plan, undertake an investigation involving pulling named lolly sticks out of a container.
Problem-solving
Improve mathematical reasoning with a real-life problem

This standalone maths reasoning KS3 lesson is based on the scenario of a teacher buying doughnuts for each student in their class. Whether you wish to buy real doughnuts for your students is up to you!
Practise estimating by converting one million pounds into coins

A million pounds sounds like a lot of cash, but exactly how much is it really? During this estimating lesson pupils will convert a vague notion of ‘wealth’ or ‘riches’ into actual pound coins.
It’s an extremely useful and engaging way of encouraging learners to carry out estimations involving large numbers, mass and volume.
Algebra
Simplifying algebraic expressions without boring drills

This free simplifying algebraic expressions lesson plan for KS3 comes with an accompanying task sheet. It involves devising expressions that will simplify to produce a given result.
Rearrange equations confidently

This algebra lesson plan develops pupils’ skills so that they can rearrange equations confidently – an important skill both in mathematics and other subjects like science and design and technology.
Geometry
Allow pupils to discover Pythagoras’ Theorem for themselves

In this lesson, pupils draw tilted squares and find their areas, then use these values to draw conclusions about the lengths of oblique lines on a square grid – leading to a statement and proof of Pythagoras’ theorem.
Use geometry to define the attributes of shapes around us

Remind your students that maths isn’t just about numbers with this detailed lesson that encourages pupils to take a closer look at what we know about geometry, and polygons in particular.
What makes a parallelogram a parallelogram? Can you mathematically define the attributes of a shape and use this to decide whether, say, something that looks like a rhombus actually is one?
Boost 3D shape understanding by making a children’s toy

This lesson plan looks at shape sorter toys. Designing and making one can be a good challenge for those in Key Stage 3. It requires a lot of careful thought, particularly if we want to avoid any shapes fitting through the ‘wrong’ hole.
Students will have to decide which shapes to include (they can go for easy or hard options), how big to make them, and how to draw out the required nets accurately.
Use creative approaches to calculating angles of overlapping polygons

The angles created by overlapping regular polygons can be easy or difficult to calculate, depending on what information you are given.
So, taking a creative approach to important mathematical processes like this can deepen students’ understanding of the principles involved and develop vital skills of reasoning and deduction.
Explore the properties of triangles and spot patterns in a sequence

In this open-ended lesson, learners explore a sequence of gradually larger shapes and consider what mathematical questions they can ask about them.
What is the same and what is different about a group of triangles? How can we draw them accurately? What measurements make an impossible triangle, and can students work out which triangles come next in a sequence?
Show how line and rotational symmetry are linked

This lesson plan teaches students about line and rotational symmetry and how they are related, getting them to invent and draw their own shapes with particular symmetries.
Use leaning ladders to explore triangles
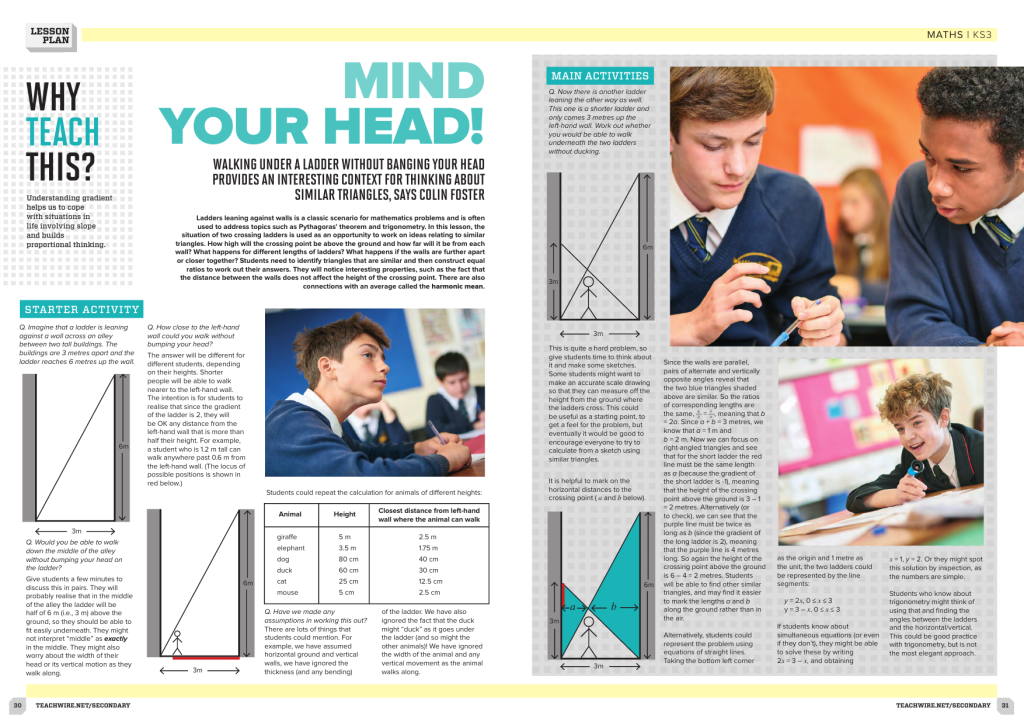
Ladders leaning against walls is a classic scenario for mathematics problems and is often used to address topics such as Pythagoras’ theorem and trigonometry.
In this lesson, the situation of two crossing ladders is used as an opportunity to work on ideas relating to similar triangles.
How high will the crossing point be above the ground and how far will it be from each wall? What happens for different lengths of ladders? What happens if the walls are further apart or closer together?
Work out the topic area by finding three angles of a triangle

Learners are often asked to practise finding the third angle of a triangle when the other two are given. In this lesson they get the opportunity to work on the topic area by finding all three angles according to different constraints.
KS4 maths lesson ideas
Geometry
Use perimeters and Pythagoras’ Theorem to calculate the shortest route
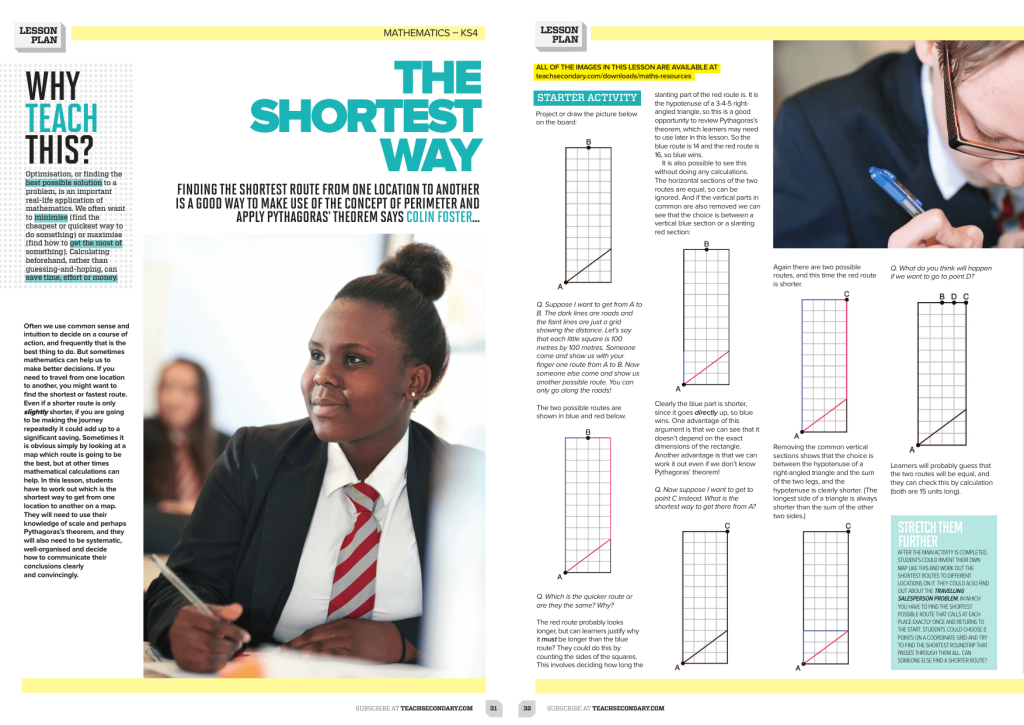
Applying their knowledge of scale and Pythagoras’ Theorem, in this lesson students are tasked with calculating the shortest route between two destinations on a map and explaining their reasoning as clearly as possible.
Use Pythagoras’ Theorem to find accurate values for triangle perimeters

In this lesson, students use Pythagoras’ theorem to find accurate values for the perimeters of some triangles.
Although the values of the perimeters are so close that it would be very hard to distinguish them by measurement, mathematics makes it possible to be absolutely sure about the order in which they come.
Explore two successive geometrical transformations
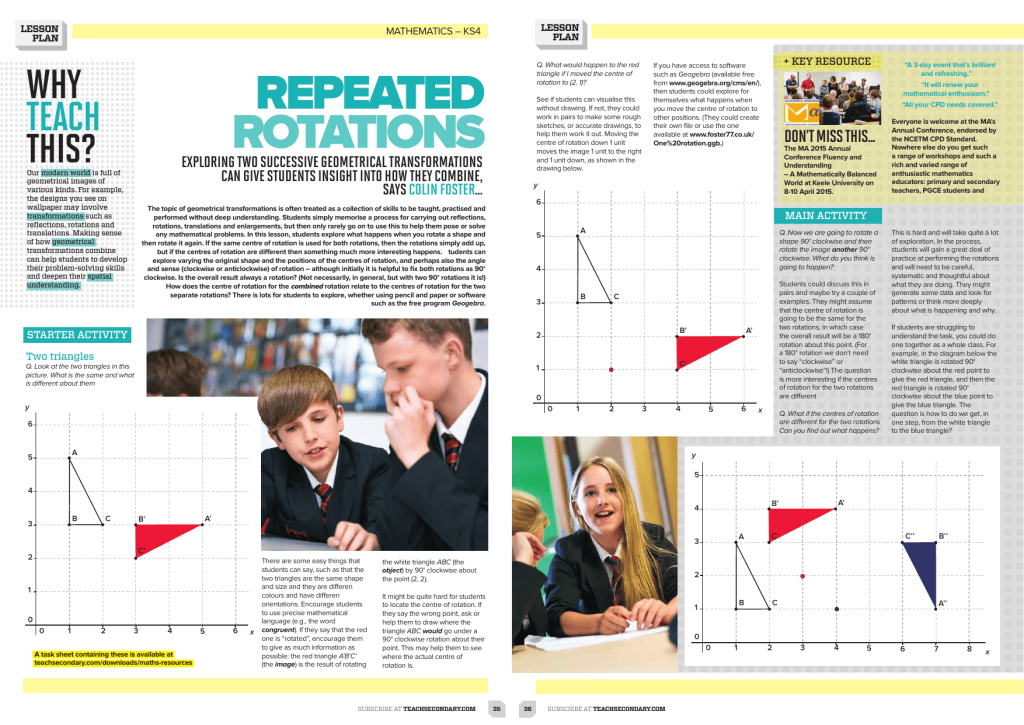
Traditionally, pupils are taught geometrical transformations by learning a set of skills they can apply to reflecting, rotating and enlarging shapes without giving the process too much thought.
But what if they were to called upon to use those skills to solve a mathematical problem? In this lesson that’s precisely what they’re tasked with doing…
Understand how shapes move when broken down into points and lines

In geometry students need to use their spatial reasoning and visualisation skills to understand the shapes and how they will move when broken down into points and lines.
This lesson allows pupils to look at two fixed points and how they relate to other points.
Statistics and probability
Examine the effects that margins of error have on time, distance and estimation

This lesson sees students examine the effect that margins of error can have on otherwise seemingly clear results.
Starting with the seemingly clear result of a race, students look at how multiple inaccuracies in the measurement of distance and time can combine to produce a very different – and even counter-intuitive – outcome.
Number
Show the connection between HCF and LCM

This lesson takes the ideas of highest common factor and lowest common multiple, which are often taught separately, and deals with them together to help learners to appreciate the connections between them.
Calculate rate and time by exploring how long it takes multiple people to paint a wall

This lesson is about calculating how long it will take to paint a wall if several people work at it at the same time. Will it take less time with more people helping? And if so then how much less?
Students need to make assumptions that are realistic to the real-world situation, but they also have to make assumptions that will make the calculations easy to do and give an answer that is close enough for practical purposes.
Embed adding and subtracting fractions into a richer problem

They’ve been taught the technique a dozen times or more, but through embedding it within a richer problem, ‘adding and subtracting fractions’ might finally make sense to students with this lesson plan.
Use ratio to calculate how to carry enough food in the desert
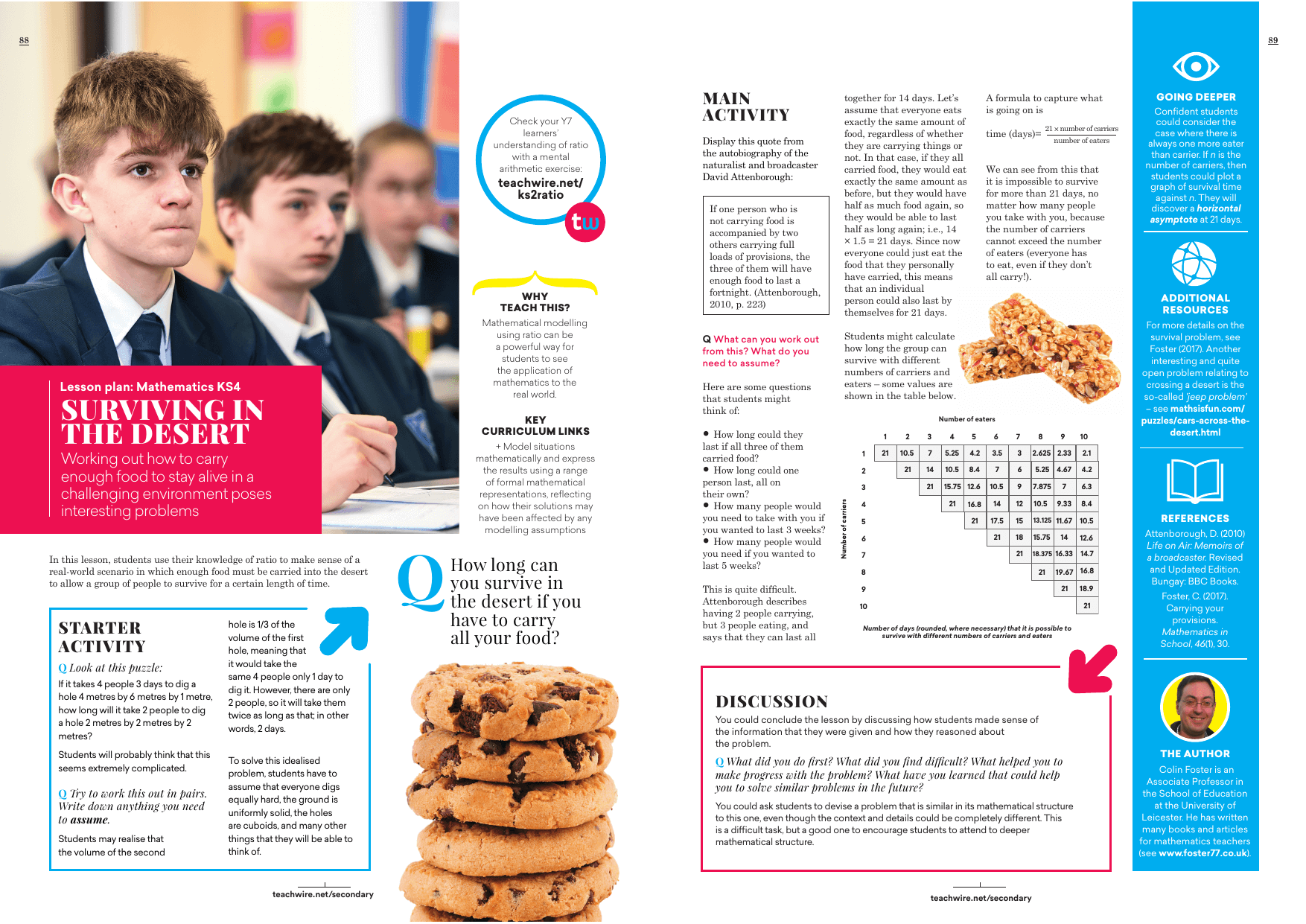
In this lesson, students use their knowledge of ratio to make sense of a real-world scenario in which enough food must be carried into the desert to allow a group of people to survive for a certain length of time.
Algebra
Use algebra to find out why a number trick works

In this lesson, algebra is used to make sense of a number trick that the teacher performs. Students are asked to explore the mechanics, experiment with some numbers, and then use algebra to try to probe exactly how and why the trick works.
This lesson provides an opportunity to work on expanding brackets and simplifying algebraic expressions, as well as making sense of the final answer in terms of the place value of the original numbers.
Bring together a host of mathematical ideas and techniques

Quadratic expressions are considerably more complicated to work with than linear expressions, and students often find them hard to handle.
In this lesson, students approach factorising non-monic quadratics by trying to find factorisations which will expand and simplify to produce a quadratic expression of a specified form.
This entails lots of useful practice at expanding pairs of brackets and collecting like terms, and also gives opportunity for students to unpick what is going on, so as to gain insight into how the inverse process of factorising works.
Construct your own quadratic equations

This factorsing quadratics maths lesson helps students become confident and fluent with techniques such as factorising quadratics by offering a scenario in which they need to construct their own quadratic equations in order to solve a bigger problem.
Shade graphical linear inequalities by locating mystery pairs of coordinates

This lesson teaches shading graphical inequalities, but not as a sequence of instructions to follow, as it is often done. Instead, asking learners to find a ‘mystery point’ can bring the process to life.
Statistics and probability
Explore probability by playing dice games

In this lesson, ask students to estimate the probability of winning a game in which they throw an ordinary dice and move a counter that many spaces forwards.
To win, they must ‘hit ten’ by landing on the tenth square from the start. This game is too complicated for students to work out the probability of winning theoretically. Therefore, they must estimate it by playing the game several times and seeing how often they win.
This enables them to calculate how much money they might be willing to pay to play the game, if the prize for winning is £1.
Illustrate the limitations of bar charts

In this lesson, you task students with devising bar charts in a deliberately misleading way, by splitting data concerning visitor numbers at a sports centre into different categories.
However, when pupils use the same data to plot histograms, it will soon become clear that their ability to show frequency density helps to communicate an accurate sense of what the data distribution really is.
Problem-solving
Link maths to real life in this maths lesson about money

Mathematical questions about a photo in a carpark gives a real-life context to this maths lesson. Students will devise their own investigations about the photo that will involve money, algebra, and finding patterns. Students will also need logical thinking and careful arithmetic in this KS4 maths lesson.
Use flowcharts to set up rules about iterative operations

Flowcharts are a highly visual way of communicating information. We use them in this lesson to set up rules about operations that will be performed iteratively.
Invite students to explore what happens when they put different numbers into a given flowchart. Later, experiment with varying the features of the flowchart themselves. They will encounter some converging sequences and use algebra to predict and explain the outcomes.
Maths homework worksheets

Help students practise their maths skills with these free maths homework question packs for Year 7, Year 8, Year 9 and GCSE maths.
More maths resources
- Algebra games and GCSE maths games to play online and offline
- More KS3 maths games and lesson ideas










