Effective models for directed number teaching in secondary maths

What's the best way to teach directed numbers so that students can understand? Don Steward takes you through the various models he's tried over the years…
- by Don Steward

My own efforts to teach the topic of directed number arithmetic have passed through three distinct phases, personal traditions, all with an equally held conviction at the time that they were ‘the best’.
Guiding models were utilised with the same ambitions: to offer a teaching sequence that develops a structure of related ideas, built with a purposeful methodology.
I wanted, as all teachers do, a majority of students to (i) be initiated: offered a basis for their belief (a conceptual framework) and (ii) attain consolidated ideas: a decent semblance of procedural skill facility in working on directed number calculations, across a range of contexts.
Initially at least, practical references are likely to help locate the ideas of extending a number line below zero and counting ‘backwards’.
With stairs you can go up and down and go down (below zero) to the cellar. Lifts go above and sometimes below the ground floor; thermometer readings also go below zero.
What happens when you go above and below sea-level (with a clearly demarcated zero)? Bank accounts allow overdrafts – what does it mean to be in debt? Pacing or jumping forwards and backwards is sometimes a feature of games (like ‘hopscotch’).
These are often helpfully introduced in earlier education and students usually seem able to appreciate the notion of extending a number line through zero, backwards and also identifying that eg –3 is the opposite of +3, both being the same distance from zero, linking this to symmetry.
They have experienced it in their lives. Although time only goes forwards; walking, running and skipping can be reversed, beyond an origin.
Quick routines
These ideas may be helpful in identifying the existence and a need for negative numbers to describe situations. They might also support plausible reasons for the result of adding and in some cases subtracting them. But they seem of limited value if they cannot help to firmly establish and justify addition and subtraction procedures and also lead on to quick routines being appreciated for directed number arithmetic.
Although helpful to counting, ordering and some calculations, negative numbers become useful things through their more formal and abstract operations, in all forms of calculations and when used to shorten strings of algebraic terms.
Through my own fairly regular mistakes with algebraic and arithmetical work, even though I’m quite proficient, it is evident that the arena is error fraught.
Research emphasises a range of difficulties, from mere slips to an extreme of systematic conceptualisation errors, particularly with subtracting a negative number.
Many problems stem from overgeneralised applications of positive integer arithmetic and can lie in students not quite appreciating subtraction beyond ‘taking away’ amounts.
Some students initially find it strange and problematic that a sign (+/-) can be used both as a unary operator (applied to a single number) eg –(+3) is –3 and also as a binary operator, eg (+3) – (+6) is -3.
Some teachers keep the ‘number’ in brackets with a sign for a while, to help understanding in early encounters and to help appreciate which buttons to press on a calculator (negate: (–) and subtract: – ).
Effective model
So, what is highly desirable is an effective teaching model, to make sense of all directed number calculations.
This model can then be available if an automated response fails. Any model used will ideally extend to multiplication operations and algebraic manipulations.
It is in Year 8 that my main desired impact of the maths curriculum over the year was to integrate and solidify the various aspects of dealing with directed numbers.
As well as with a main opportunity to introduce the topic (over a week), exposures arose substantially in connection with straight line graph relationships, reflection using coordinates in all four quadrants and many other tasks, eg linear equations and negative enlargements – wherever they could be sensibly slotted in.
An ambition was to avoid the obstacles that loom later on without this skill facility.
I shall briefly consider three such models that appear commonly and that I have used at various stages, in my time order:
1. Robot stepping
‘Facing and pacing’ introduced to me through an article by Peter Chilvers in Mathematics in School (14.1), in January 1985. ‘Sam the sentry’ moves according to spoken instructions: facing forwards (as a default) or backwards (‘about turn’) then moving forwards or backwards, so many paces. Students playing with LOGO programmes helped to firm up these ideas.
2. Annihilation Counters
Introduced, apparently, by Caleb Gattegno and employing a neutralisation notion (‘annihilation’), together with accompanying equivalence classes (a ‘black/red’ pair can be introduced) that can be used to make sense of calculations. The notion of ‘holes and sandcastles’ is associated with this model.
3. Vectors (1D and 2D)
This has similarities to ‘robot steps’ in that movements on a number line are considered. Urged by Hans Freudenthal in 1905 (chapter 15 of Didactical Phenomenology of Mathematical Structures). A vector approach extends to multiplication through dilatations (eg in negative enlargements).
A brief description of the first two models:
Robot steps
A sentry or a robot follows a clear set of instructions. Associated with a number line, the robot always starts and returns to a ‘home’ position: at zero.
They always start by facing in the positive direction (conventionally to the right). A negative sign in-between step commands tells the robot to turn and face left (‘about turn’).
Cards can be put on the wall to remind students about which direction to face (either + or – ). Moving commands are put in brackets to identify them as such and involve pacing. So, eg (+2) means go forward two steps, (–3): backward three steps. Students can enact a few examples:
- (+3) + (–5): three steps forward; and remain facing +; and then move five steps backwards: ends up at (–2)
- (+2) – (+3): two steps forward; and face the negative direction; and then three steps forward: ends up at (–1)
- (+4) – (–3): four steps forwards; face the negative direction; three steps backward: ends up at (+7)
- (–5) – (–7): five steps backwards; face the negative direction; seven steps backwards: ends up at (+2)
There are benefits to this model: it can be fun to do at the front of a classroom; correct results are obtained, following a bit of practice; facing the negative direction and walking backwards results in a move in the positive direction which is a helpful notion.
However, there are concerns: the middle sign merely says which way to face, so the operational quality gets lost. The moves result in a position on a number line which is the effective move (vector) that would get you to this place in one go (from zero).
I’m not sure that this idea of combining movements was clear to students. The mixing of moves and positions on a number line seemed unproblematic after a while. It can be used to help understand what goes on with multiplication:
- (+2) × (–3): move two lots of backwards three, facing the positive direction: is (–6)
- (–4) × (+3): move four lots of forwards three, facing the negative direction: is (–12)
- (–2) × (–5): move two lots of backwards five, facing the negative direction: is (+10)
The direction to face when multiplying is (maybe arbitrarily) shown by the sign of the first number.
So, all operations can produce correct results (as division is closely associated with multiplication) and the idea of ‘direction reversals’ is a helpful one.
However, overall it seemed a bit of clumsy model. As well as introducing notation that will later be dropped (the brackets around the step command), the model mixes and muddles operational signs (the ‘imperative’, steps) as positions on a number line (the result) and with movements (vectors).
It also did not seem to be a helpful model for students to refer back to because the structure was insufficiently simple.
Counters
This model is advocated by James Tanton in his work on ‘holes’ and ‘piles’. It is used in the MARS (2015) ‘adding and subtracting directed numbers’ and described with several examples by NRICH (5947).
It relies on a principle that negative (red) and positive (black) counters annihilate each other (like matter and anti-matter, adding and taking from a pile).
Addition is reasonably straightforward to comprehend:
- (+7) + (–3): 3 reds annihilate with 3 blacks resulting in 4 blacks: (+4)
- (–4) + (–5): 4 reds and 5 reds is 9 reds: (–9)
- (–6) + (+1): 1 red will annihilate with the 1 black leaving 5 reds: (–5)
Some subtractions are also straightforward (where you don’t bridge through zero):
- (+7) – (+3): 7 blacks subtract 3 blacks is 4 blacks: (+4)
- (–8) – (–3): 8 reds subtract 3 reds is 5 reds: (–5)
Other subtractions involve ‘creating a pair from nothing’ eg: (+4) + (–4) is 0
- (+7) – (–2): 7 blacks subtract 2 reds, I can’t – so I’ll add 0 to the 7 blacks in the form of (+2) + (–2) which leads to (9 blacks and 2 reds) subtract (2 reds) which is 9 blacks: (+9).
- (–6) – (+4): 6 reds subtract 4 blacks, I can’t – so I’ll add 0 to the 6 reds in the form of (+4) + (–4) which leads to (4 blacks and 10 reds) subtract (4 blacks) which is 10 reds:
(–10). - (+3) – (+5): 3 blacks subtract 5 blacks, I can’t so I’ll add (+2) + (–2) to the 3 blacks which leads to (5 blacks and 2 reds) subtract (5 blacks) which is 2 reds: (–2).
- (–5) – (–8): 5 reds subtract 8 reds, I can’t so I’ll add (+3) + (–3) to the 5 reds which leads to (3 blacks and 8 reds) subtract 8 reds which is 3 blacks: (+3).
This model of opposites annihilating each other can also involve having a combination of black and red counters presented as a group which are then partitioned by a squiggly line, put in various places. Nrich 5947 details several examples of these.
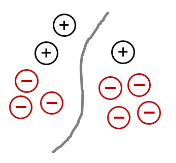
The whole (ie all of the 10 counters) is –4.
The diagram, with this particular squiggly line, can be interpreted as showing that:
- left part + right part: (–1) + (–3) is (–4)
- whole – left part: (–4) – (–1) is (–3)
- whole – right part: (–4) – (–1) is (–3)
And the squiggly partition line can be drawn in various other places, enabling three other statements to be explored and appreciated.
This ‘counters’ model involves pair-annihilation and pair-forming. All appropriate results for addition and subtraction of directed numbers can be formed. The operations of addition and subtraction are respected.
Whilst the techniques aren’t superficial, the notions are helpful (utilising inverses) and simple enough to reconstruct. The processes can be made visual.
However, although I preferred this approach to ‘facing and pacing’, there are concerns: the introduction of a ‘zero’ pair form is neat but the whole notion of ‘counters’ is one step removed from relationships with a number line and can’t easily be extended to multiplying directed numbers.
Although reasonably content that these two models were beneficial, enabling students to reason about directed number arithmetic and providing meaning to the rules which control operations, I moved on. I shall outline my now preferred third model teaching approach, that of vectors, in a further article.
Don Steward is interested in effective tasks for teaching mathematics to 10-18 year old students. Read more from him on his blog at donsteward.blogspot.co.uk.
This article is the second in a series on directed number teaching. You can read part one here and part three here.











