Using a Vector Approach to Directed Number Teaching for Unity, Coherence and Consistency
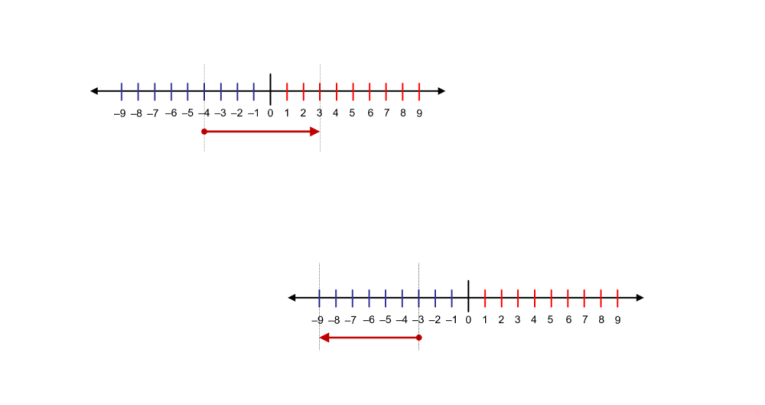
Viewing a sum as a move to an end point from a start point on a number line can help your students grasp directed numbers effectively, says Don Steward…

- by Don Steward

An apparent historical reluctance to engage with negative numbers, to the habits of the pre-1700CE European mind at least, perhaps highlights some of the difficulties that there are in working abstractly with directed number arithmetic.
Progress seems to have been made through generalising equation solving techniques and by considerations related to number lines particularly when involved in a coordinate system (as well as in commercial arithmetic).
What is needed for students, As Judy Larsen advocates, is phenomenological guidance in order to avoid epistemological obstacles.
Two models that seem to support work towards symbolic mastery were outlined in the second article: ‘robot steps’ movements along a number line and positive/negative ‘counters’ – the latter closely linked to ancient Chinese practical arithmetic with coloured sticks.
A third model, very similar to the first, utilises directed magnitudes on a number line. Hans Freudenthal has argued that the number line is a ‘device beyond praise’ and that it lends meaning to rules which prevail operationally.
He also details a recommendation that this number line might better be presented horizontally rather than vertically – so that the symmetry is clearer and the lines more naturally extendable. All maths classrooms would probably benefit from having a directed number line, above the board at the front of the room.
Before considering a third (‘vectors’) model for developing a knowledge of directed number arithmetic, three other approaches that aid a deliberately faceted teaching approach seem worth mentioning:
1. Pattern extending This involves an extrapolation of number statements from a sequence that lends validity to rules that Freudenthal (drawing on Hankel’s remarks) refers to as ‘the algebraic permanence principle’: it fits with a sequence of statements so it is desirable that it should be so:
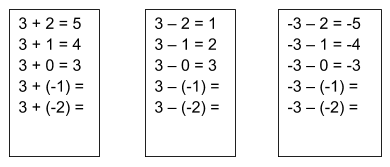
2. Extending functions This is closely allied to pattern extending. Plotting points that fit the relationships: y = 3 + x or y = 3 – x or y = –3 – x etc ought to continue as a straight-line graph, integer points maintained into negative territories.
The ‘geometrical-algebraic permanence principle’, a term also used by Freudenthal, indicates how algebra has been shaped by what is visually apparent or obvious, removing what could be argued to be arbitrary definitions.
3. Utilising symmetry Jemma Sherwood argues for more substantially involving the symmetry properties of movements on a number line with directed number arithmetic. This seems to have merit:
- -5 – –3 can be viewed as the opposite (ie reflection in the origin) of 5 – 3
- -4 – 2 as the opposite to 4 + 2
- 5 – –3 as the opposite to -5 – 3
Students could be provided with a directed number sum and asked to explore the reflections (through the looking glass) of these: ‘what might this look like backwards’?
A vector model
This is essentially based on Chapter 15 of Hans Freudenthal’s book Didactical Phenomenology of Mathematical Structures. Although temperature difference as a model offers a helpful reference, negative temperature gains are a little too curious to be credible.
However, all of the right ingredients – involving displacements with a direction as well as a magnitude – are present.
In positive integer arithmetic and now, for a subtraction sum, time needs to be spent thinking and talking about a ‘gap’ perspective: viewing a sum as a move to an end point from a start point.
So, for example, 3 – (-4) is the gap between 3 (the end place) and -4 (the start place). This gap is (+) 7 because you move to the right.
At another time students might also explore this relationship of ‘the difference between’ and consider the equivalence of displacements on a number line.
For subtraction, 8 – 5 is the same sum (and so has the same result) as 3 – 0, 2 – (-1) and -7 – (-10).
Without altering a result, a subtraction can be transformed (shifting the gap to a simpler location) by adding/subtracting same amounts (ie to the subtrahend and minuend).
So, eg 3 – (-4) is equivalent to 7 – 0 (by adding 4 to both). You might place -4 – 5 in the middle of a board and ask students to suggest sums that are the same as this, maybe in a spider, then consider how the sums have been transformed.
The equivalence of pairs of points on a number line when considering subtraction is defined by an equal length and direction.
With algebra, it is stating that: a – b ≡ (a + c) – (b + c) and also ≡ (a – d) – (b – d).
For addition, it can be helpful to think about a start position on the number line and then a movement (to the right or left) by an amount.
So, eg 7 + (-9) can be thought of as starting at 7, and then moving 9 spaces to the left, which results in arriving at the end position, of -2.
This can be linked to an all-vector interpretation: starting from the origin (0) with a vector of +7 (ie 7 steps to the right) followed by a move of -9 (ie 9 steps to the left) is equivalent to a vector of -2.
In work on trying to teach directed number I ask students to attempt to record both the ‘start, journey, end’ and the ‘start, end, journey’ statements – even though this might initially be confusing.
This ‘vector’ model differs from ‘robot steps’ in considering the twinned aspects of ‘gaps’ (end, start, movement) and ‘journeys’ (start, movement, end). For consistency, ‘robotic movements’ always involves ‘start, move, end’ with an in-between minus sign changing the direction.
So, -5 – -7 for ‘robot steps’ would be interpreted as starting at (-5) then moving 7 steps backwards but in a reversed direction (thus adding 7).
Accepting a loss of consistency, I seek to involve both ‘gaps’ and ‘journeys’; I do this because students seem to appreciate both perspectives and they do suggest both aspects in deliberations.
A blurring or fuzzing of vectors and positions on number lines also seems an important understanding. Beyond that, I hope that these twinned statements also contribute to an understanding that given a + b = c you also have other equivalent (and related) statements, including c – a = b.
Considering the forms of language used, I’m not convinced that is too helpful to always distinguish between positions on a number line (as ‘negative’ 2) and an operation (as ‘subtract’ or ‘minus’ or ‘take’ 2)
Personally, I prefer to just use the word ‘minus’ for quite a lot of the time, mainly because this seems to extend to later work in algebra where eg the contents of a bracket are negated.
What does seem important whatever the approach and language used, is that students appreciate that a negative sign reverses (direction) so that, in general, b – a = –(a – b) and also that –(-c) = c.
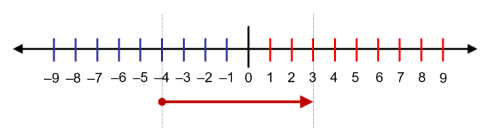
Younger students have some familiarity with negative numbers. In starting off with a more abstract consideration of directed number operations I present diagrams like the one above and ask them to tell me a ‘story’ about what is going on.
For this diagram they usually say: A start at (-4) followed by a journey of (+7) results in an end of (+3).
This can be recorded as -4 + 7 = 3 and the teacher might write this in response to what a student has said.
Or, given time and an encouragement to consider alternatives, they also say: The gap between the end (+3) and the start (-4) is a journey of (+7). This can be recorded as 3 – (-4) = 7.
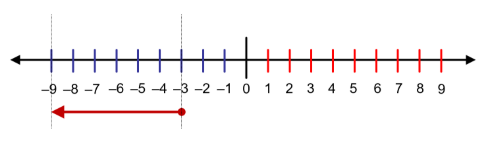
For the diagram above,
- ‘Start, journey, end’ is: (-3) + (-6) = -9 and
- ‘Start, end, journey’ is: (-9) – (-3) = -6.
With all-vector interpretations, a negative sign reverses the direction (as in ‘robotic’ ‘about turn’).
By involving this preferred ‘vector’ model and the twinned aspects of [end – start = movement] and [start + movement = end] I intended to achieve gains in understanding as to both how and why adding and subtracting with directed numbers works.
As Caleb Gattegno advocates, this ought to lead to gains in symbolic mastery – over time, general forms and structures ought to be appreciated.
Gaining in proficiency seems the next step and should leave the model behind – although hopefully remaining in touch with it to inform and enlighten any mistakes, doubts or misconceptions.
I shall include ideas for gaining proficiency and appreciating how to multiply (and so divide) directed numbers in a final article.
I shall do no more here than flag up a fourth model that was advocated by Pierre van Hiele and actively promoted by Freudenthal, claiming that, for vectors, ‘in one dimension these objects and their operations lack badly needed relief’.
Van Hiele maintained that an involvement of 2-dimensional vectors and the parallelogram rule for composing and decomposing them was most helpful in considering how directed number arithmetic works.
Subtracting a vector reverses the direction but not the magnitude (adding the opposite). Utilising 2-D vectors goes some way to overcoming what Freudenthal describes as the didactical asymmetry between positive and negative numbers.
The positive numbers are what students experience in their earlier schooling and so become more important through their familiarity. Negative numbers are introduced as the result of operations, as a secondary object. They are cold temperatures, overdrafts and negative attitudes.
Whatever model is adopted (or adapted) the aim is the same: that students appreciate how extensions to negative numbers are made (in counting and ordering), that negative answers are as important as positive ones and that when operating with and on negative numbers there is some (visual) model in which to embed and cultivate understanding.
Although some rules (and definitions) could be viewed as arbitrary (playing within an abstract and formal mathematical game) there ought to be a compelling story being offered for a student to view directed number arithmetic as normal and natural.
Don Steward is interested in effective tasks for teaching mathematics to 10-18 year old students. Read more from him on his blog at donsteward.blogspot.co.uk.
This article is the third in a series on directed number teaching. You can read part one here and part two here.










