Teaching Negative Numbers – Some History on Embracing Negatives and Directed Number Teaching
In the first of a four-part series on teaching directed numbers, Don Steward looks at how various cultures approached negative numbers in mathematics throughout time…

- by Don Steward

More readily than others, some Ancient societies, in China and India, seem to have had fewer qualms about engaging with negative numbers, incorporating them into their mathematical thinking as well as detailing arithmetical procedures.
This disposition now seems eminently sensible. Whilst widely accepted for accounting purposes it is curious that other societies were far warier of involving them in more general mathematical work.
Mathematical understanding evolved, with negative numbers popping up fairly regularly, mainly when solving linear equations and as an alternative solution to quadratic equations.
One plausible reason for a divergence in accommodation may be due to those cultures appearing to better appreciate duality and zero, in their religious thinking as well as in financial transactions.
Whatever the reason, a historical steer for using negative numbers came substantially from the East, with the West being reluctant to accept them.
Neither the Babylonians or the Egyptians seem to have been interested in, or entertained, negative quantities.
Other peoples were similarly hitched to practical measurement considerations: lengths and areas, so regarding positive numbers as the only ‘proper’ ones.
Although the Ancient Greeks shifted mathematics into more abstract and rigorous realms, these remained rooted in geometrical diagrams and so did not permit negative solutions to problems.
Euclid managed to inoculate against negative numbers in all his texts. Accordingly, Diophantus (~250CE, Alexandria) attempted to shut the door firmly on them by claiming that the problem of finding a number so that four times it, add 20 makes four was more than unsolvable, it was “absurd”.
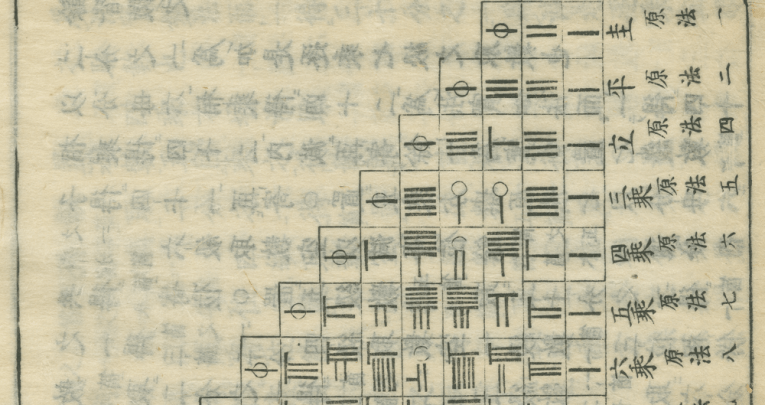
Before that, the Chinese had used negative numbers and outlined clear rules for combining them, with apparatus and instruction for calculating with them.
This was necessary both for commercial arithmetic and for their solution method for solving simultaneous equations (in several variables) contained in the ‘Jiuzhang Suanshu’ – a compilation of mathematical techniques collected over a period probably between 1000 and 200BCE.
Liu Hui added an illuminating commentary on this text (~260CE). Chapter VIII of what is referred to as ‘Nine chapters on mathematical art’, reduced an array of numbers to a triangular form, utilising negative number arithmetic in the process.
For example, Liu stated that to subtract (add) a certain number means to add (subtract) the same number of the opposite sign.
In that time, there was a counting system that could be manipulated physically with red bars signifying positive integers (‘Zheng’) and black bars positive ones (‘Fu’) – the opposite of our present day ‘being in the red’.
Moving on around 800 years, Brahmagupta, a Hindu mathematician (~600CE) detailed 11 rules for dealing with gains (fortunes) and loss (debts).
These rules included (rule number 5): a debt subtracted from zero is a fortune and (rule number 9): a product or quotient of two debts is a fortune.
He used a dot above a number to denote that is was a negative quantity and was able to multiply out (a – b)(c – d) correctly.
Moving away from arithmetic, Bhaskara considered and presented negative roots to quadratic equations – but then he dismissed them. He was the first to record negative numbers related to a number line – as movements in a ‘contrary direction’.
The famous Persian mathematician Al-Khwarizmi (~800 CE) was influenced by translations of Brahmagupta’s writings. Guided by this, in one of his more arithmetical works, he used the notion of debts and fortunes for inheritance calculations.
However, in his more ‘algebraic’ treatment of quadratic equations (but not using symbols) he followed Euclid in steering clear of negative numbers, detailing three separate techniques for solving types of quadratics that had just positive coefficients eg:
- n2 + 10n = 39
- n2 + 21 = 10n
- n + 12 = n2
Following Al-Khwarizmi’s work, in money considerations, Abul-Wafa (~970 CE) gave general rules for combining ‘debts’ and ‘fortunes’ giving an example where a subtraction of 5 from 3 gives a ‘debt’ of 2 which he multiplies by 10 to obtain a ‘debt’ of 20, which when added to a ‘fortune’ of 35 results in 15.
It was clear that adding and subtracting are opposites (converse operations) so, by the turn of the first millennium, negative numbers were seen to be useful in arithmetic, more predominantly in financial matters and still widely dismissed in ‘algebra’ which continued to derive its legitimacy from geometrical considerations, essentially steeped in Euclid’s influence.
The tacit understanding of proof/justification was and remained ‘visual’ and so connected to geometry for much of the next millennium.
Across Europe there was a softening hesitation to accept negative numbers:
- Fibonacci (~1228) allowed them in accounting problems but not others;
- Chuquet (~1484) obtained negative roots to quadratics and used negatives as exponents but still referred to them as ‘absurd’;
- Stifel (~1500) also called negative numbers ‘absurd’ but did use negative number coefficients in equations;
- Cardano (~1550) referred to ‘true’ and ‘false’ numbers but needed to engage with the square root of negative 15 to obtain a solution to a cubic equation;
- Viete (~1570) didn’t like them but did state that to take away a defect is to supply it;
- John Wallis (~1660) lent some insight into negative number arithmetic by using a number line and associating calculations with movements right and left.
By the 18th century negative numbers were not only more acceptable but operations with them were treated more rigorously.
- Euler (~1740) appealed to symmetry in suggesting that –a × –b could not have the same result as –a × b or a × –b so must have the same result as a × b.
- Hamilton (~1830) detailed principles for using directed number using a θ in front of a number (from the Latin oppositio) to denote a negation, so (importantly) if n = B – A then θn = A – B
‘If it be said that the square of -5, or the product of -5 into -5, is equal to +25, such an assertion must either signify no more than 5 times 5 is equal to 25 without any regard for the signs, or it must be mere nonsense or unintelligible jargon.’
Maseres’ dismissal seemed based on an inability of mathematicians of that time to point to a physical analogy, particularly for multiplication.
One evident reason for a (positive) shift of attitude towards negative numbers was Descartes’ introduction of a coordinate system (~1600) and the subsequent (slow) emergence of analytic geometry – reworking tried and tested geometrical methods obtained from reading the Ancients, geometry moving home so that it became progressively expressed in terms of algebra.
There was an increasing need for negative numbers for a fuller view of functions (curves) and to enable and automate a wider range of equation solving techniques.
No longer did people identify various types of quadratic equation and cubic equations – a neater synthesis was available where a variable (x) could take all values.
Possibly as important, the emergence and development of calculus in the 17th century had a need for negative numbers.
By the 19th century, directed magnitudes had been introduced and mathematicians including De Morgan, Peacock and Hamilton had worked on the validity of basic operations eg:
If x = ab + (–a)(b) + (–a)(–b)
by factorising the last two terms:
x = ab + –a(b + –b)
x = ab + –a(0)
x = ab
and by factorising the first two terms:
x = (a + –a)b + (–a)(–b)
x = (0)b + (–a)(–b)
x = (–a)(–b)
so, ab = (–a)(–b)
Some of the historical concerns about negative numbers were quite justified. Removing deliberations from their tangible (geometrical) roots, ground rules for operating with negative numbers needed to be re-negotiated (as Dick Tahta outlines in MiS May 1995 volume 24.3).
It matters which way round you subtract: 3 – 8 ≠ 8 – 3.
The associative law needs to be treated cautiously: with 7 – 3 – 8 needing to be staged in correct order (left to right). Both of these concerns seemingly resolved by replacing – n with + – n.
The square root of a negative number presents problems, as it does for other functions: y = 3x is fine in terms of a smooth, continuous graph but y = (–3)x behaves strangely (even more so for fractional exponents). It is no coincidence that the imaginary numbers developed alongside the uses of negative numbers.
Antoine Arnauld (~1660) was rightly concerned that the ratio of a lesser to a greater could be equal to one of a greater to a lesser eg 2 : 3 = –2 : –3. This did seem very absurd. Leibniz suggested that the numbers could not be compared in this way but he stated that this equivalence was allowable in a calculation.
At advanced levels, Johann Bernoulli corresponded with Leibniz about arguments that included:
- (–1)2 = 1 so 2 log (–1) = 0 and so log (–1) = 0. Euler later establishing that log(–1) is imaginary
- putting 2x = –1 there is no such value for x
- the integral of dx/x is the integral of –dx/(–x) so log (–x) is log x
An acceptance and intertwining of negative numbers as (i) numbers (ii) positions on a number line, extended through zero and (iii) as directed magnitudes (displacements or vectors drawn from mechanics) is a relatively recent development, needing some considered refinements.
The basic rules of calculating with negative numbers now seem relatively simple and obvious, firmly established as logical – albeit requiring calm and caution when calculating with them! Directed numbers came in out of the cold.
Don Steward is interested in effective tasks for teaching mathematics to 10-18 year old students. Read more from him on his blog at donsteward.blogspot.co.uk.
This article is the first in a series on directed number teaching. You can read part two here and part three here.










