Develop Mathematical Thinking by Making Pupil Talk a Central Feature of Lessons

Clearly the mathematical content learnt is important, but other ‘learnings’ may be equally important, says Mike Askew…

- by Mike Askew

Many readers will be familiar with the current interest in teaching in Shanghai and what we can learn from practices there. As a university teacher, I’m also keen to see what research has to say about what might make a difference.
Reading a paper about this recently, I was struck not only by similarities in the aims of mathematics teaching that are being promoted in China – including more independent and investigative tasks and discussion – but also by some key differences in terms of beliefs about teaching and learning.
Research often focuses on teaching in only one country. Even when teaching across countries is looked at, it’s rare for research to compare matched lessons due to differences in curricula and how schools are organised.
So I was interested to come across research that did exactly that in the form of an article by Huang, Prince, Barlow and Schmidt in volume 26.1 of The Mathematics Educator.
The researchers report on observing the same lesson (in the sense of having matched goals and tasks), one in a city in southern China and one in a city in south-eastern USA.
The lesson was built around a series of tasks that involved looking at patterns in calendars, leading to a focus on mathematical generalising and reasoning – what the researchers describe as ‘cognitively challenging’ tasks.
For example, the lesson started by asking pupils to circle three dates in a row on the calendar, add them and give the total to the teacher, who could then tell them what the separate three dates were.
Pupils had to try and work out how this ‘trick’ worked, then went on to explore whether other patterns and generalisations were revealed through tasks such as circling five dates in a row or three dates in a column.
Pupils exploring
One of the findings was that by the end of the Chinese lesson, the teacher had got through more of these pattern-finding tasks than the American counterpart.
Although the Chinese teacher tried to engage pupils in the task, they ended up pointing out the generalisations to the pupils. The teacher ‘dominated’ the talk, with little opportunity for pupils to explain or justify patterns.
This was in spite of China’s relatively recently revised teaching standards that explicitly encourage less direct teaching and more pupil exploration and independent thinking. In the American lesson, pupils got through fewer tasks but had more opportunities to engage in mathematical exploration and thinking.
As is the nature of much research, several questions remain unanswered. Most important is whether the pupils learnt more in one lesson than the other.
The differences in these lessons seems to be partly rooted in different views of the overall aim of mathematics teaching. If your aim is to impart to learners as much mathematical knowledge as possible, then why not teach it directly?
With such a perspective, pupil contributions are likely to be seen as not central to the teaching, but more as a means of checking understanding and, perhaps, keeping the class engaged.
If, on the other hand, you see your aim as helping pupils develop as mathematical thinkers, then pupil talk is more than a nicety and has to be a central feature of the lesson.
When thinking about which set of pupils learnt more, it’s worth considering the breadth of things that might be learnt through these different approaches. Clearly the mathematical content learnt is important, but other ‘learnings’ may be equally important.
For example, pupils may learn to listen to each other, not just the teacher, or learn that mathematical reasoning may initially be a struggle but through that struggle you can figure things out for yourself.
Teaching is not a neutral task. How we teach brings about multiple learnings, many of which go beyond the mathematical content.
Beauty and power
When planning maths lessons, it’s easy to focus primarily on the content details of the national curriculum, but it’s helpful to keep reminding ourselves of what the aims of our curriculum are. These explicitly include, according to the DfE, ‘the ability to reason mathematically, an appreciation of the beauty and power of mathematics, and a sense of enjoyment and curiosity about the subject’.
There is also an explicit expectation that pupils are ‘assisted in making their thinking clear to themselves as well as others’, implying that much classroom talk needs to come from the pupils.
In practice, this means that we need to plan at least some lessons around the idea that pupils need to be doing most of the mathematics and talking about what they are doing, not simply watching or listening to a teacher doing it.
Thinking about ‘tasks’ as what teachers set for pupils to do, and ‘activity’ as what pupils subsequently do helps make clear who is doing what in a lesson. Opening up the gap between task and activity is one way of getting pupils to ‘do the maths’.
What is…
The work of Marion Walters and Stephen Brown is an invaluable framework for developing teaching tasks in ways that encourage pupil activity. Their basic approach is to write two lists.
The first features all the elements of a task (including even the obvious ones) and is called the ‘what is’.
The second list – the ‘what if not’ – is based on the first and focuses on how changing some of the task’s givens might lead to further mathematical activity.
Take, for example, this simple task around the theme of ‘doubles: 25 + 25 = [ ]

Not all of these ‘what if nots’ looks particularly promising, but some possible tasks that might now be offered include:
Find at least three different ways to complete each of these open sentences:
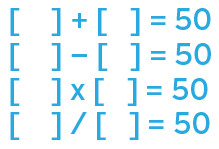
Find at least three different ways to complete each of these open sentences:
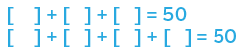
Write down three different multiples of 5. Double each of your multiples. What do you notice? Check if this still happens with three other multiples of 5. Can you explain why this happens?
The national curriculum states that maths is a ‘creative and highly interconnected discipline’. Introducing pupils to playing with tasks through trying out ‘what if nots’ is a great way to get them thinking about being creative.
After all, if I want my pupils to be the ones doing the maths, I might as well extend that to getting them to create some tasks.










