Algebra games – Offline & online maths ideas for KS2-4
Maths is essentially all just one big puzzle book anyway, so why not have some fun?
- by John Bee
There are loads of ways to try new maths concepts, and games are naturally one of the most fun. Here’s a selection of easy offline and online algebra games that your class will enjoy…
We formally introduce algebra into classrooms in Year 6. However, you can informally introduce algebra all the way back in Early Years. As well as adding an element of fun to your teaching, playing games will help pupils develop a range of skills, including:
- turn taking
- listening
- critical thinking
- problem solving
- collaboration
Algebra games with Cuisenaire rods
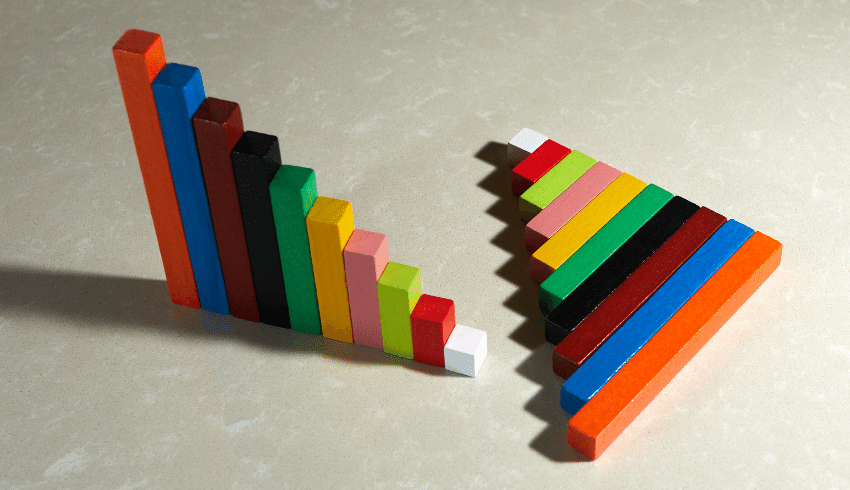
One of the ultimate ways to introduce and play games which require thinking algebraically is to use Cuisenaire rods.
Give children some time to play with the rods, allow them to explore how they may fit together. Ask them to make staircases and give each block a numeral value (white = 1, pink = 2, etc…). This may lead on to an understanding that 2W = P (2 white cubes = 1 pink cube).
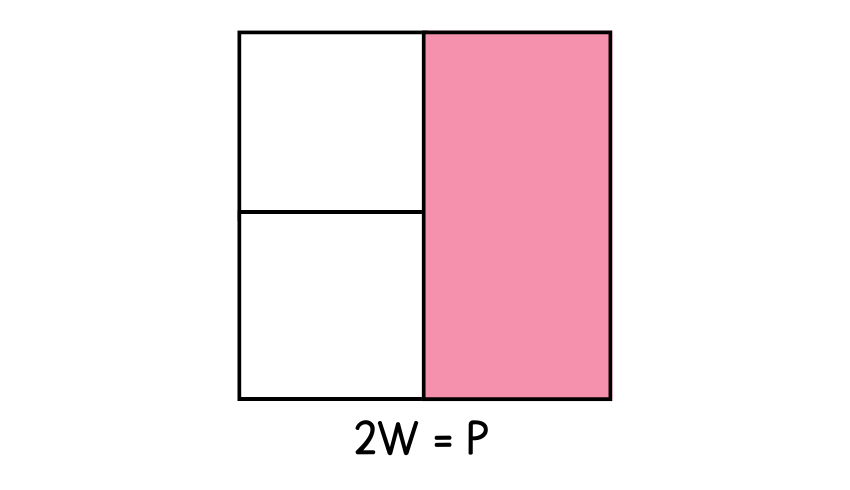
You can now experiment with how many white rods make a different colour rod. Children can make some notes around this (6W = Dark G, for example).
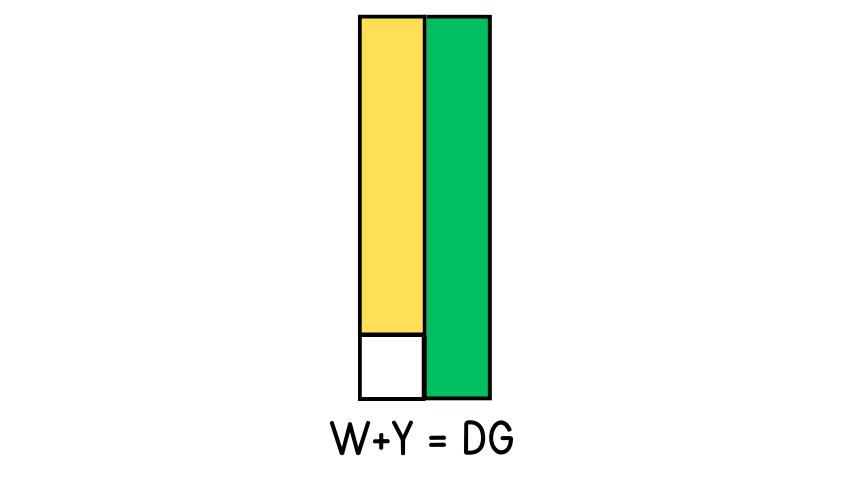
Children can then look at how combinations of rods can be equal to others (for example, white + yellow = dark green or W+Y = DG). Note down the relationships you spot.
Filling in numerals/letters
Deepen understanding by giving children a print-out of numerals zero to nine in block form. Ask pupils to find out which numerals they can fill using Cuisenaire rods. For an extra challenge, ask children to use a specific number of rods for some of the numerals. For example, it’s possible to fill the numeral six with exactly six rods.
Alternatively, use our letters resource and ask children to cut out and spell their name, initials or the name of a loved one/pet using Cuisenaire rods.
Once children have filled in their numerals or letters, they can write an expression to show what it is made up of. For instance, 5 = 3G + Pur + Pink + W.
Colour block algebra game
Children can develop this further using a colour block worksheet game. Print out our worksheets on A3 paper and cut round the cards. Place the cards face down.
Children need to pick a card (numbered one to ten) and then colour in squares on the grid using the Cuisenaire colours. The coloured in section should be in a straight line, to match the Cuisenaire rods. Pupils should add their initials to each square they colour. The winner is the person with the most colours on the board.
Cuisenaire rods, combined with play, are a great way to strengthen and deepen algebraic thinking. Children can have hours of fun and you can rest assured that you’re building solid foundations to support them in the classroom.
John Bee is head of KS2 and maths leader at a primary school. Follow John on Twitter @mrbeeteach and see more of his work at mrbeeteach.com
More offline algebra games
Algebra substitution game to play in pairs
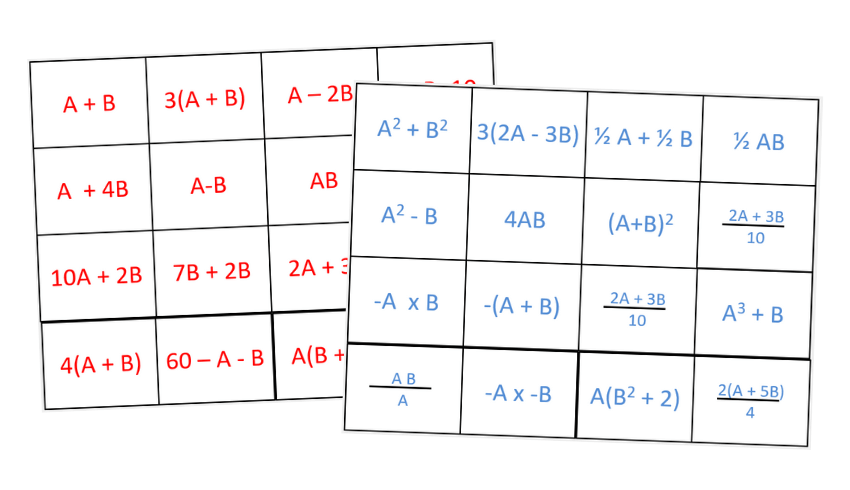
This free algebra substitution game resource gets pupils working in pairs and practising substituting values into expressions.
Students each roll two dice – one to give a value of a and the other the value of b. They then work out the value of the expression for their values. Whoever has the highest puts their colour counter on the square. The winner is the person with the most counters on the board at the end.
Dara and Achi games
The below games, Dara and Achi, are effective starting points for teaching children to analyse patterns and relationships.
They focus pupils’ attention on representations, before more formal algebra begins. Games like these extend thinking beyond recall or memorisation and introduce logic, variables and critical thinking – all essential skills when working with algebra.
Dara maths game
The ancient game ‘Dara’ involves recognising patterns and mathematical relationships among numbers, objects and geometric shapes. You can use it for a range of ages from KS1 to secondary,
This two-player abstract strategy game is played on a 5 x 6 board. Each player has 12 pieces (counters) in their own colour. The goal of the game is to capture all of your opponent’s pieces.
The game has two phases: the drop phase and the move phase. In the drop phase, players add (drop) their pieces onto the 5 x 6 board. Once they’ve placed all their counters, the move phase begins.
Players take turns moving one of their pieces to an adjacent empty square. If a player moves one of their pieces to create a row of three, they capture one of their opponent’s pieces. You can move horizontally or vertically but not diagonally. The game ends when you capture ten of your opponent’s counters.
Achi maths game
The boardgame ‘Achi’ is similar. Here, you have four counters each and take turns placing them onto a 3 x 3 grid of linked circles. Once you’ve both placed all your counters, you can slide your counter along a line horizontally, vertically, or diagonally.
The winner is the first person to get three in a row. This is a game of strategy and encourages pattern spotting.
Connect 4 algebra worksheet for KS3/KS4
This KS3/4 connect 4 algebra worksheet involves pupils working in pairs. The aim is to get a connect four on the question sheet. Both pupils must complete each question – the person to choose the box wins the box if they get it correct, but if they don’t get it correct and their partner does, they win the box.
Factorising equations bingo for KS3/4
This bingo algebra game come with 40 different bingo cards, a PowerPoint of questions and a teacher checklist so you can verify the winning card.
Celebrity murder mystery KS3 algebra lesson
This muder mystery KS3 algebra game covers expanding single brackets, substitution, nth term and solving equations. The download includes an introduction, clues, an extension activity and answers.
Online algebra games
Shuttle Mission Pro
The website Math Playground has a whole host of interactive online games. The game Shuttle Mission Pro introduces pupils to the concept of scaling and balancing equations to calculate the weight of aliens. It requires some complex strategic thinking.
Function Machine
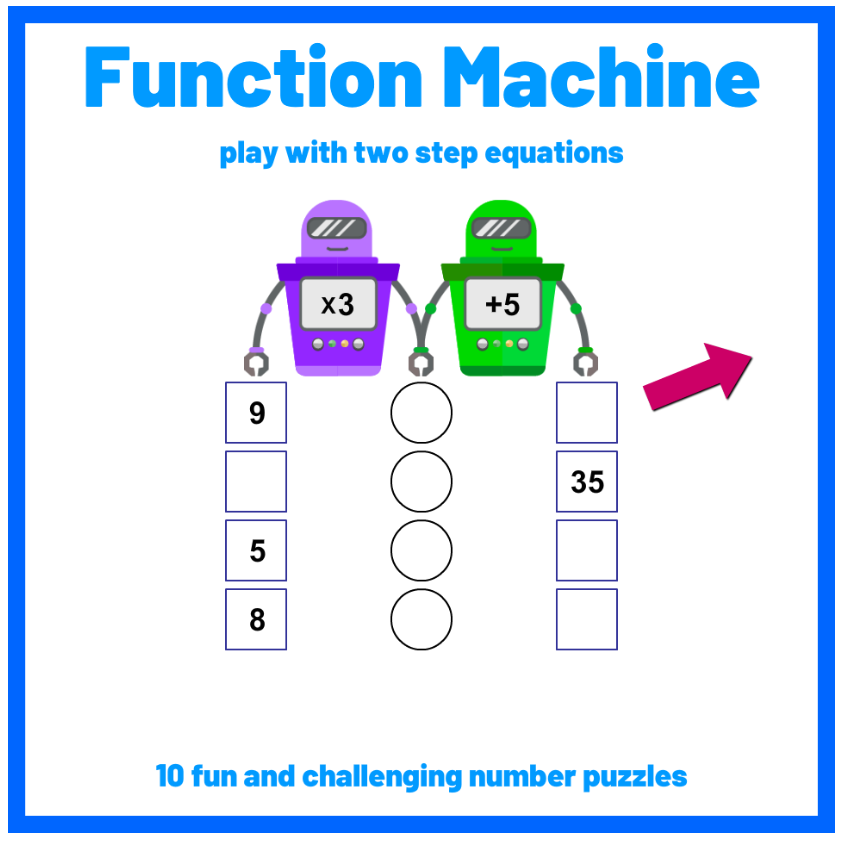
Games using function machines allow children to experience sequences when exploring algebra. Function Machine has three different levels, two-step function machines, decimals and integers. It’s great for consolidating understanding of function machines and algebraic thinking.
Function Builder
Function Builder is an impressive game that is an interactive simulation of function machines and how they work. Children can use patterns, numbers or equations and there’s great engaging visuals.
Who Wants to be a Hundredaire
Who Wants to be a Hundredaire is based off the television quiz show (is it still going? It can’t be, can it?). It involves answering square root questions to work your way up to the top prize of $100, which apparently you don’t actually win no matter how many times you email the company to demand it.
Algebra Noodle
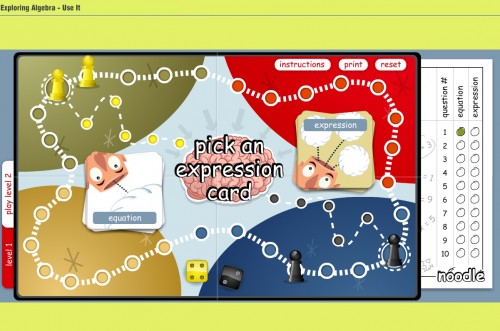
Board-game enthusiasts will dig this little gem. Move your pieces around the board faster than the CPU player, and knock them back spaces by landing on their piece. All by correctly answering algebra questions.
Model Algebra
This mental maths game helps pupils to practise solving visual equations where letters stand for numbers. First model the equation, then make zero pairs, then solve for X.
Number Patterns
This fun game helps Year 6 pupils sharpen their numeracy skills. They have to generate ordered pairs based on a given rule and also identify a pattern from a list of ordered pairs. This will stand children in good stead when it comes to solving more complex number problems in secondary school.
Otter Rush
A romp of otters (yes, that is the collective noun) is racing down the river. Pupils need to practise exponents by choosing the correct answer to power their otter over land and sea. How quickly they answer will determine how fast their otter will go. Otterly adorable.
Linear Function with Intercepts
On this page, students need to interpret a word problem to find the related linear equation with an intercept. The answers are multiple choice.
Browse maths games KS1 and maths games KS2 ideas or our list of GCSE maths games.
