Understanding sine – How to explain this basic trigonometric ratio for KS3/4 maths
Russell Timmins breaks down sine into easily digestible pieces…

Trigonometry, to a lot of intelligent people, can be something of a mystery.
Initially, we should start to see it as a way of solving problems with right-angled triangles. And the key to solving such problems is to fully understand the three basic trigonometric ratios, which we will from this point on refer to as ‘trig ratios’.
The three trig ratios in question are sine (sin), cosine (cos) and tangent (tan). In this article however we are going to concentrate for the most part on sine.
The reference angle in a right triangle is, in general, given the symbol θ (theta). This angle is always the most important place to start when problem solving with trigonometry because the sides in relation to it determine whether sin, cos or tan should be used.
In this image we are looking at a general right triangle from which the important three trig ratios can be defined.
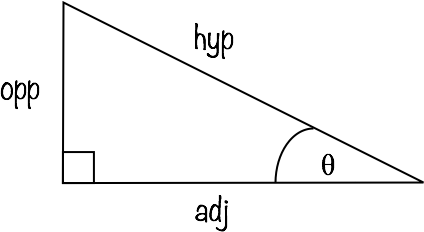
From reference angle θ we label the side opposite to it ‘opp’ or ‘o’, the side next to it ‘adjacent’, ‘adj’ or ‘a’ and importantly, the longest side is always the hypotenuse ‘hyp’ or ‘h’.
The longest side is directly opposite to the right angle, which is also the largest of the three angles.
The sine of angle θ is the ratio, ‘opposite side : hypotenuse’, and as in any ratio this can be converted to a fraction, like this:
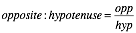
Now as with any ratio of two values, both can be scaled up and down by a multiplier, which effectively creates a ‘zoom in or out’ effect. In this next image we can see how two triangles of clearly different sizes can be similar to each other (respective sides are different, but angles are the same) because of the identical ratios of the same two sides in each one.
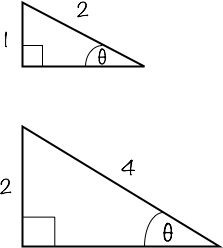
In both triangles we can say that sin θ is defined as both 1⁄2 and 2⁄4 which of course are equivalent fractions.
In this example we can physically place the smaller triangle inside the larger one.
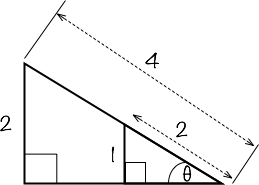
How do we know that we can place one triangle inside the other? We know because the ratio of the opposite side to angle θ and the hypotenuse is the same on both triangles and as such θ will not be affected by the change in the sides’ lengths. In this example sin θ = 30˚ and here is the proof of this.
Draw an equilateral triangle with side lengths 2.
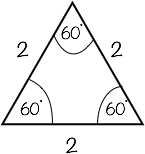
Form a right angled triangle by dropping a perpendicular from the top vertex. This halves the top angle 60˚ to 30˚ and halves the base to 1.
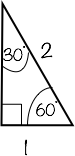
Now without the use of a calculator we can find the true value of sin 30.
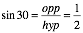
In this example we can state categorically that if the ratio of the opposite side to an unknown angle (θ) and its hypotenuse are 1:2 or if you prefer 1⁄2 then the angle will always be 30˚. In a graphical or scientific calculator the sine of every angle is given either as a decimal or fraction. I intend to develop the reasoning further in a later article that brings the importance of circles into trigonometry.
To recap however, sin θ is a ratio of the opposite side to the angle and the hypotenuse on a right-angled triangle. What it is not, is an angle in its own right.
Useful application of sin 30
If you want to construct an angle of 30˚ but you do not have a protractor, draw two lines perpendicular to each other and measure 1 unit (a unit can be any length you choose, and hence 2 units will be twice as long) on the upright side. From that point measure 2 units on your ruler and bring this point down to where it touches the base side (see image below) and you will have an approximate angle of 30˚. Try this as an experiment to see if it works.
Russell Timmins is a maths education author, adviser, trainer, lecturer and blogger. You can find him at his Making Maths Easy to Understand Blog (mathsolutionz.org) and follow him on Twitter at @mathssolutionz.










