Square numbers – Activities and resources for KS2

Use these ideas to allow pupils to experience the concept of square numbers, thus strengthening their understanding…

- by John Bee
- School improvement adviser & mastery specialist for Maths Hubs Programme Visit website

These square numbers activities are designed to help you start with the concept of square numbers and take small steps to develop, strengthen and deepen understanding.
They use a concrete, pictorial and abstract approach to allow pupils to experience the concept, thus making it more secure and memorable.
These square numbers activities will also help children to reason, make links, look for patterns and hypothesise.
They should arrive at the generalisation that a square number is a number which is multiplied by itself. This is the end point; the generalisation; the rule.
Children will have been on a conceptual journey of discovery to arrive at this end point, rather than it being one of many abstract mathematical rules.
What are square numbers?
Square numbers are integers that can be expressed as the product of a whole number multiplied by itself. In other words, they are the result of squaring a whole number.
For example, 4, 9, and 25 are square numbers because they can be written as 2×2, 3×3, and 5×5, respectively.
Teaching for conceptual understanding
Teaching for conceptual understanding requires children to understand how and why a concept works, rather than passively accepting abstract rules a teacher presents to them.
Explaining to children that square numbers are numbers multiplied by themselves is the final generalisation.
Lots of teaching, learning and construction of a concept must come before. Deepening concepts and starting with ‘why’ is a powerful way to develop and strengthen understanding.
Activities for teaching square numbers
Activity 1: Why a square is a square

As this concept focuses on square numbers which are linked to square shapes and properties of shapes, it may be worth starting with a discussion on the properties of a square. Hand out this 2×2 table and ask pupils to fill it in as a starting point, thinking about why a square is a square:
Activity 2: Visual representation of square numbers
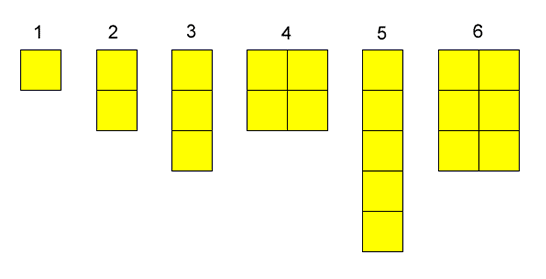
Using squared paper, invite children to draw squares ranging from 1×1 to 12×12 in size. Ask pupils to calculate the area of a square they’ve drawn. Explain that this is a square number. This visual representation deepens pupils’ understanding while exposing the structure of the concept as a calculating area.
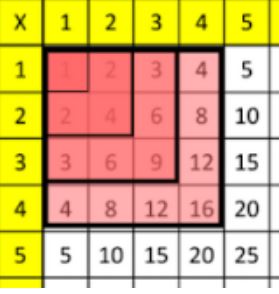
Alternatively, provide children with this multiplication grid and invite them to draw squares, starting from one in the top left-hand corner and increasing in size each time. Look at the number in the bottom right-hand corner to identify the square number.
Activity 3: Square, rectangle or stick
Ask children to draw a 1×1 square on squared paper. Now, add one extra 1×1 square and see if you can create a square, rectangle or stick. Keep adding on extra 1×1 squares.
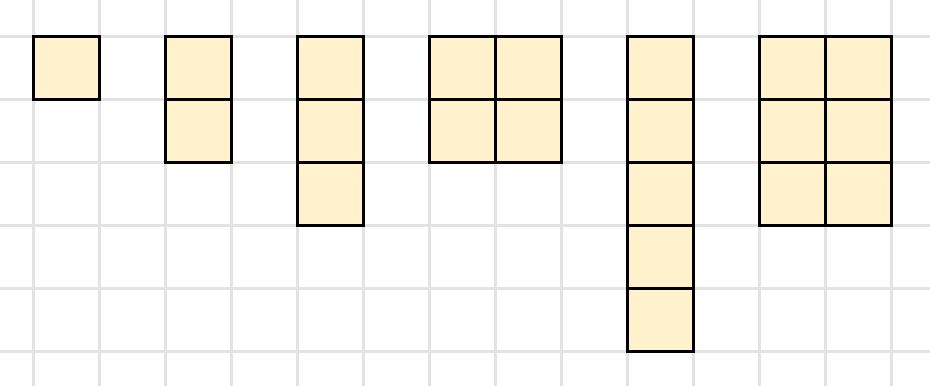
Make a note on this worksheet of how many 1×1 squares you need to create squares, rectangles and sticks.
Pupils should notice that they can only make squares from 1, 4, 9, 16, 25 (etc) squares. Alternatively, ask children to cut out squares and manipulate them on their work area to investigate this activity in a more concrete way.
Activity 4: Shade the grids
Explore the structure of square numbers and allow children to look for patterns by giving pupils three grids: 0-100 in rows of 10; 0-99 in rows of nine; 0-96 in rows of eight.
Ask children to shade in the square numbers. What do they notice? The numbers go from no real pattern in the 10×10 grid to being lined up in columns in the 8×8 grid and subsequent grids after that.
Extend this by asking children to draw more grids, getting shorter by one each time.
Activity 5: Adding prime numbers
Making links and connections in mathematics is important for children to be able to reason and explain. Linking prime numbers and square numbers allows for rich discussions and the strengthening of both concepts.
After teaching or revising what prime numbers are, pose this question: can you make a square number by adding two prime numbers together?
Give children visual representations of square numbers with the number of squares visible inside each square to 12×12. Ask them to cut them out.
Show children how two prime numbers add together to make a square number, such as 11 + 5 = 16. Show this by colouring in the squares, like below:
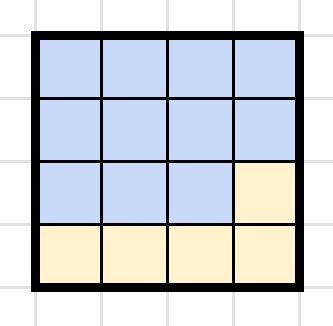
Activity 6: Adding square numbers
Now children have had time to explore the concept in depth and secure their understanding of square numbers, consider an investigation to apply understanding.
Try posing this question: which numbers can you make by adding two square numbers together? Cut out visual representations of squares to 12×12 to help.
Children who are confident can do it abstractly and systematically. For example, 1 + 4 = 5; 1 + 9 = 10; 1 + 16 = 17.
Activity 7: Think of a number
Do this activity with counters, cubes, pencil and paper or abstract notations:
- Think of a number
- Square it
- Subtract your starting number
- Is the number you’re left with odd or even?
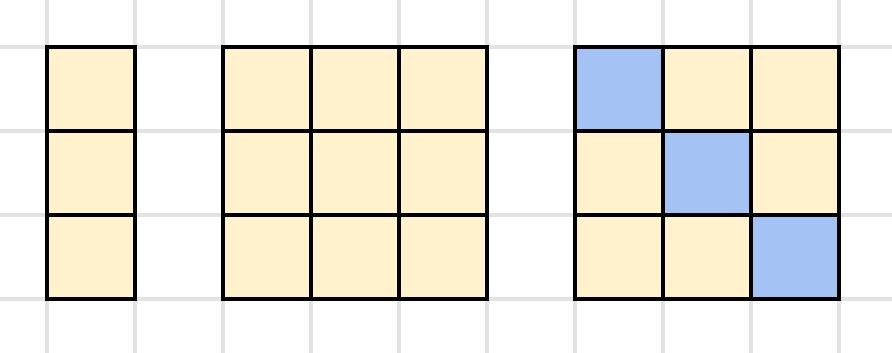
What do pupils notice? The number is always even. For example:
- Think of a number: 3
- Square it: 9
- Subtract the starting number: 9 – 3 = 6
In the example below, the blue squares show the number of parts subtracted from the square.
John Bee is head of KS2 and maths leader at a primary school. Follow him on Twitter at @mrbeeteach and visit his website at mrbeeteach.com.
Is 1 a square number?
Yes. Because 1 x 1 = 1, 1 is a square number.
What are the square numbers to 100?
1, 4, 9, 16, 25, 36, 49, 64, 81, 100
More resources for teaching square numbers
Multiplication square patterns
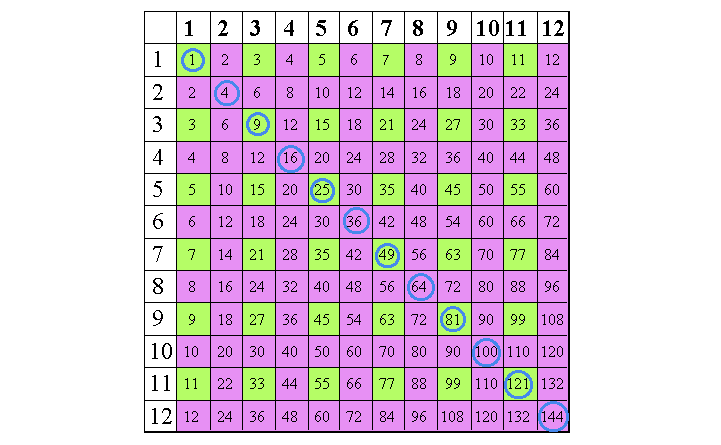
This simple activity from Teaching Ideas is a good place to introduce square numbers. By laying them out on a 100 square children can see the nice, obvious pattern of the diagonal line across the square, which can only help them understand the idea.
Use our free printable times table grid for this and other activities.
Explainer videos
If you’re after a short video explaining what square numbers are, either for pupils to watch before class, or during, then this one does the job nicely.
Alternatively, this video is a little less hi-tech, but does a good job of addressing any potential uncertainties children might have, and lays the concept out in an easy-to-digest manner.
Square numbers introduction worksheet

This simple worksheet from Primary Resources features a few questions each on:
- squaring numbers
- finding which number squared will give the target number
- area of squares
- square roots
- calculator work on finding the square root of large numbers
NRICH activities
NRICH always has a number of great activities and puzzles for maths topics, and square numbers is no different.
A few worth checking out are:
Custom worksheets

Use Primary Maths Resources to generate free worksheets instantly.
Choose between beginner, developing and expert, hit create, and it’ll give you a worksheet and answers to print. Simple as that.
More free worksheets

For worksheets on square numbers to 12, you’ll find nine free ones ready to print at Mental Arithmetic.
Square Pairs game
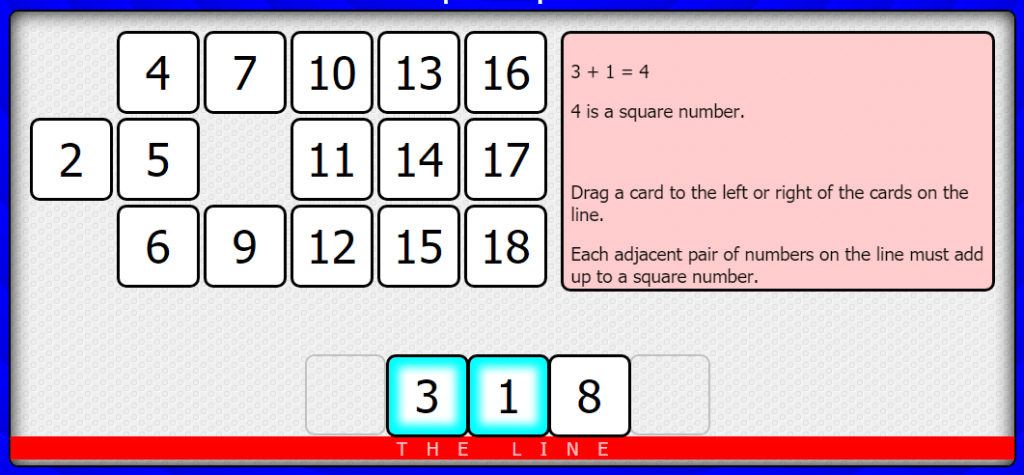
This interactive game for two players gives you a number from 1-20, and asks you to drag another one next to it on a number line so that the two add up to a square number.
Player two then does the same, putting any of the remaining numbers next to the end numbers on the number line, as long as the two numbers next to each other add up to a square number.
1-50 squares quiz
For a fun challenge try this Sporcle quiz on square numbers. You have four minutes to find the square of every number from 1-50.
Challenge students to see how many they can get right before the timer runs out.










