Area and volume – What happens to the area of a disc when the disc is enlarged?

Students can become confused when faced with linear, area and volume scale factors – but they don’t have to be, says Colin Foster…

- by Colin Foster
- Reader in mathematics education at Loughborough University Visit website

The difficulty
Imagine that you ring up and order a 20-inch pizza to be delivered. When they arrive, they say they are sorry, they don’t have any 20-inch pizzas, but they have brought you two 10-inch pizzas instead. Is that OK?
Students may worry about things like the amount of crust, the shape of the slices, or how the pizzas would be shared out, but not realise that in fact two 10-inch pizzas contain only half as much pizza as one 20-inch pizza!
The solution
Rather than explaining the point, just display the image below, without any words, and ask: What does this have to do with the pizza question?

If the diameter of the blue disc is 20 inches, then the diameters of the red discs will be 10 inches. The total area of the two red discs is clearly much less than the area of the blue disc.
Since the area of a disc is ??², where ? is the radius, Area ∝ ?², or, since radius ∝ diameter, ?, Area ∝ ?². This means that twice as big a diameter gives a disc with four times as much area. The two red discs in total cover only half of the area of the blue disc!
Another way to think about it is to imagine stretching one of the red discs until it is twice as wide, but without changing its height.

It now becomes an ellipse, with twice the area of the original red disc. This means that the area of the ellipse is equal to the sum of the areas of the two red discs.
This red area is half of the area of the blue disc, because the red ellipse would have to be stretched vertically by another scale factor of 2 for it to become congruent to the blue disc. This would take another doubling of its area to match the area of the blue disc:
Trending
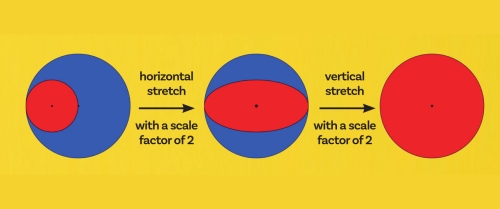
Students may think this is just a weird thing about circles, but it is actually completely general. Whenever any 2D shape is enlarged, for the enlarged version to remain similar to the original shape, it must be stretched by the same factor ? both horizontally and vertically.
Each of these stretches increases the area by a factor of ?, so overall the area will increase by a factor of ?².
Checking for understanding
To assess students’ understanding, ask them to imagine scaling up a sphere in 3D. What would happen to the volume?
Multiplying the radius (or diameter) of a sphere by a factor of ? will require three stretches this time, in order for the new shape to be spherical (i.e., similar to the original sphere). The three stretches, each with scale factor ?, in all three perpendicular directions, will scale up the volume by a factor of ?³.
Colin Foster (@colinfoster77) is a Reader in Mathematics Education in the Department of Mathematics Education at Loughborough University and has written numerous books and articles for mathematics teachers; for more information, visit foster77.co.uk










