KS2 maths – Make word questions more approachable

Questions about eggs in boxes and change from shopping can tie pupils in knots, but by using this approach to mathematical word questions, you’ll soon see an improvement
It’s so common for children to make great strides in KS2 maths, but then be inconsistent when it comes to answering multi-step word questions.
Keen to quickly find an answer, pupils will often skim-read the information given in a question, focusing mainly on the numbers provided.
They look for the first clues as to the correct operation to perform, often making errors or missing important steps.
In contrast, an expert problem-solver may take longer processing and representing the information that is given in a question.
They can consider whether an answer is realistic. They may even have the capacity to course-correct if they make a mistake.
Worded maths questions
The research paper ‘Removing opportunities to calculate improves students’ performance on subsequent word problems’ (Givvin, Moroz, Loftus & Stigler, 2019) has helped me to see how all children can learn to break down word questions.
If pupils are given all the information in a word question in full, they have a lot of data to process all at once, which can be a significant barrier.
Also, children often don’t think about the mathematical structure of the question as they quickly try to calculate the answer.
But what if the information in a worded question was revealed more gradually? This limits the amount of detail that needs to be processed in any one moment.
Also, by making it impossible to calculate an answer straight away, children are forced to think about the structure of the question.
They can predict the extra information that they might need. Or given all the information, children can guess what the question could be.
We might not show numbers, so children can calculate different possible answers.
Suddenly, what was previously a closed question becomes an interesting, open task!
Let’s consider an example ‘slow reveal’ prompt, where to begin with we’ve concealed parts of the question behind coloured bars, like this:
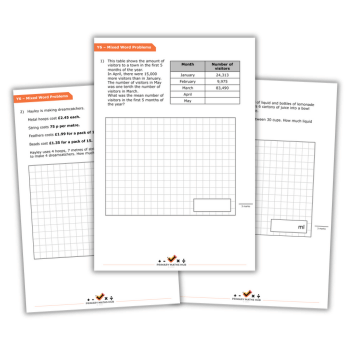
Step 1
Pencils: 20p Rubbers: 15p


Here, I can start by reading the information and asking, ‘What could the question be?’ and, ‘If that’s the question, what would the information be?’
The children might suggest it’s, ‘How much does it cost?’ or, ‘How much change does she get?’.
We can model some simple question-answer combinations as examples.
Step 2
Pencils: 20p Rubbers: 15p

How many rubbers can Jen afford?
The question is revealed. To be able to answer this question, what information is needed? What could the missing information be?
At this stage, we can recognise that we will need to know how much money Jen has.
We might ask a question like, ‘If the missing information is Jen has 50p, what would the answer be?’
Step 3
Pencils: 20p Rubbers: 15p
Jen has £1. She buys ___ pencils and some rubbers.
How many rubbers can Jen afford?
Now we have all the information, but one number is still hidden. This allows us to calculate different possible answers. Some children might find all the possible answers!
We could represent one example answer with a bar model:
Jen could buy 4 pencils and 1 rubber

| 20p | 20p | 20p | 20p | 15p |
Step 4
Pencils: 20p Rubbers: 15p
Jen has £1. She buys 3 pencils and some rubbers.
How many rubbers can Jen afford?
Finally, we can reveal question in full. By now, all children have a much deeper understanding of the question.
Division KS2
A classic division context for children in KS2 maths is to explore is eggs in egg boxes.
Trending
Typically, for a given number of eggs, we will ask, ‘How many egg boxes do we need?’.
Often, we want pupils to identify from the context what to do with any ‘remainder’ eggs.
Are they supposed to round up or round down? Here’s an example of how to explore this context.
At each stage, you can use counters to model the calculation if required.
Step 1
The farmer packs ____ eggs into boxes.
Each egg box can hold 6 eggs.

Here, we can ask, ‘What could the question be?’ or, ‘What different questions could be asked?’.
Step 2:
The farmer packs ____ eggs into boxes.
Each egg box can hold 6 eggs.
How many egg boxes can we fill?
Now that children know the question, they can give a possible answer. Often, they will choose to work in a number range that is comfortable for them, for example choosing 12 eggs.
Step 3
The farmer packs ____ eggs into boxes.
Each egg box can hold 6 eggs.
How many egg boxes can we fill?
Answer: 3 boxes
This time, rather than giving the number of eggs, we could give children the answer and ask, ‘How many eggs could there be?’.
Now there are different possible answers. Can children find them? There could be 18 eggs. But there could also be as many as 23 eggs!
Step 4
The farmer packs ____ eggs into boxes.
Each egg box can hold 6 eggs.
How many egg boxes do we need to hold all the eggs?
Answer: 3 boxes
For the final step, we make a slight change to the question. Now, if there are any remaining eggs, we round the answer up.
By making only a small change to the question, and by keeping all the other information the same, children can see the difference between the two questions.
You can change the challenge in the number range used as appropriate, and again the answer(s) can be modelled using counters.
By revealing the information in word questions slowly, or by making small changes from one version of a question to the next, we help to slow down children’s thinking and create rich opportunities for discussion.
In using this technique, I have seen pupils experience less anxiety when working through word questions, as they have had more time to process the information.
It can also support children with English as an additional language (EAL) to identify the meaning of key terms.
Finally, it helps all pupils to understand and explain the process of breaking down a multi-step question.
I hope it’s a useful tool for you too!
Gareth Metcalfe is director of I See Maths Ltd. Follow him on Twitter @gareth_metcalfe