BODMAS – Why we should be using BOPS instead

Virtually every secondary school student in the UK has encountered the order of operations acronym, but there's a problem; it doesn’t always work…
- by Owen Elton

What does BODMAS stand for?
The BODMAS acronym stands for: brackets, orders, division, multiplication, addition, subtraction.
It is sometimes known as BIDMAS (with ‘Indices’ instead of ‘Orders’) or PEMDAS in America (with ‘Parenthesis’ and ‘Exponents’).
BODMAS rule
This mathematical rule dictates the correct order of operations to be followed when you complete a mathematical number sentence question with different operations.
The first step is to do anything in brackets, then orders next (such as square root or indices). Division and multiplication are on the same level, meaning they are given equal priority, and should be done from left to right. This is rather than all division, then all multiplication.
Similarly, addition and subtraction are on a level together and should be done from left to right.
JUMP TO A SECTION
Unteaching the rule
I began my teaching career at Highgate School. Youthful, untrained, and not yet balding, I was thrust into the steepest learning curve of my life.
Weekly meetings with my head of department were vital for discussing pedagogy and I clung faithfully to his instructions. Of uppermost importance was this one: “We never, ever use BODMAS”.
Not using BODMAS was less easy than you might imagine. Students arrived well-versed in its application.
We had to unteach it. We had to persuade rooms full of teenagers that they had to alter the fundamental tenets of their arithmetical belief system. This was difficult because teenagers hate change and they hate adults proselytising.
So why on earth would we bother? What had convinced an entire department that they should exert so much effort on such a seemingly trivial matter?
BODMAS is wrong. That’s what.
Why BODMAS is wrong
Its letters stand for:
- Brackets
- Order (meaning powers)
- Division
- Multiplication
- Addition
- Subtraction
So we’re supposed to simplify a mathematical expression in this sequence.
BODMAS examples
For example, to evaluate 3 + (3 + 3)3 ÷ 3 – 3 x 3 we proceed in the order above:
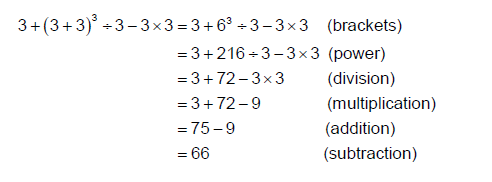
This would be a useful algorithm if it worked in every situation, but consider this simpler expression: 1 – 2 + 4 .
It contains no brackets, powers, division, or multiplication so we’ll follow BODMAS and do the addition followed by the subtraction:

This is erroneous. The correct value is 3. BODMAS has failed us. Shame on BODMAS!
We can’t have a magic mnemonic that doesn’t always work. Suppose it decided not to work at an important moment.
“We can’t have a magic mnemonic that doesn’t always work”
Imagine trying to explain to your student that the reason they dropped a grade in an exam was that the thing that you had told them always worked didn’t actually work on every occasion.
And, in fact, one of those occasions happened to have occurred in that GCSE paper.
BOPS: an alternative
There’s no point BODMAS-bashing without offering an alternative. The error illustrated above is caused by the fact that addition and subtraction should not necessarily happen in that order.
If we have a string of these two operations we call it a sum and we should work from left to right:
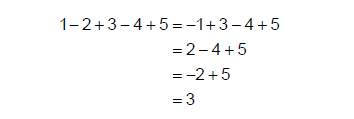
Similarly, division is no more important than multiplication. If we have a string of these two operations we call it a product and we will work from left to right again:
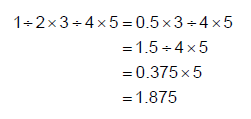
We now have the following order: Brackets, Order, Products, Sums.
This gives us BOPS which is a whole syllable shorter than BODMAS and has the considerable advantage of being reliable.
I’m sure that if someone had proposed BOPS before BODMAS then we would have consigned the latter to obscurity. Even now, it is not too late to rid ourselves of bi-syllabled arithmetic acronyms.
I call on my colleagues around the world to ban BODMAS and to purge PEMDAS. Leave no trace of them. Allow BOPS to strike a victory blow for young mathematicians everywhere.
Owen Elton is a maths teacher, a writer/performer of silly songs and author of matheminutes. You can follow him on Twitter at @owenelton.










