Teaching Highest Common Factors (HCF) – The Two Essential Stages Worth of Consideration

Highest Common Factors HCF

This blog looks at Highest Common Factors (or Greatest Common Divisors) of two or more numbers. There are two stages worthy of consideration:
- Common factors and Highest Common Factors by inspection of 2 or more numbers
- Calculating by using prime factors
Common factors of 2 or more numbers
If we examine all the factors of say, 12 and 30 we can compare results to see which factors are common to both numbers.
12 = {1, 2, 3, 4, 6, 12}
30 = {1, 2, 3, 5, 6,10, 15, 30}
We can observe that factors common to both 12 and 30 are 1, 2, 3 and 6. The highest valued factor of both of them is therefore 6. We can do this with more than just two numbers.
The same procedure can be used to find all the factors and by definition, the HCF of all three numbers.
For example look at finding all the factors of 18, 42 and 56.
18 = {1,2, 3, 6, 9, 18}
42 = {1, 2, 3, 6, 7, 14, 21,42}
56 = {1,2, 4, 7, 8, 14, 28, 56}
Factors common to all of them are 1 and 2 only, as such we can see that the highest common factor of all three numbers is 2. In other words, there is no greater number than 2 which will divide all three numbers exactly.
This method, however, can be time consuming, no matter that it will always throw out the HCF of any amount of numbers you care to use.
Calculating by using prime factors
If we break the numbers down into prime factor form we can get to the solution more efficiently. We will again look at finding the HCF of 12 and 60 to see how prime factors work in the process.
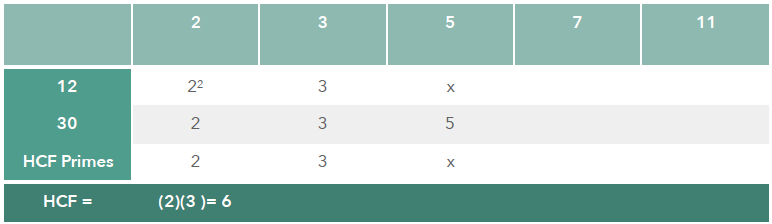
By expressing the number 12 as 22 x 3 and 30 as 2 x 3 x 5 in columns of prime values we can inspect each column to see where common primes exist, note them, then multiply them finally to see the HCF.
In the prime column for ‘2’ we see that 12 has 22 and 30 has 2.
We now need to be clear that the highest common factor of these two numbers is 2 as it is the greatest possible divisor of both 2 and 22 (4). 3 is common to both 12 and 30 and is recorded in the HFC primes column.
Later all values in the HFC primes row will be multiplied to give the HFC of the original numbers. We are left with 2 and 3 in this case which when multiplied give the product 6. We can say that no number greater than 6 divides both 12 and 30 exactly. The same approach can be used with 3 or more numbers.
We will take the earlier example of 18, 42 and 56.
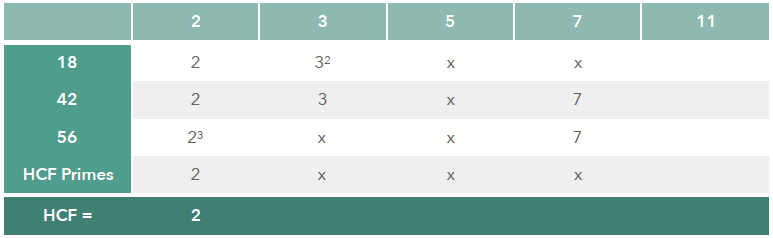
By inspection we see the only prime column that is common to all 3 numbers is 2 as 3 is only a factor of 42 and 7 is a factor of 42 and 56 but not 18.
Again there is a higher power of 2 which is a factor of 56 (23 in this case). As before we choose the lowest power in the column (2) as there is no higher power of 2 which will divide exactly all three.
Recap
When finding the HCF of 2 or more numbers practice the following stages in order.
- Convert all numbers to products of their primes
- Record the primes which are common to all numbers in the problem
- Record the lowest power that occurs in any prime column (see tables above)
HCF..or Greatest Common Divisor
This blog assumes that factors of whole numbers have been defined and understood.
When finding the HCF of two or more numbers it makes sense to write the numbers in question as products of their respective primes.
For example as a product of their primes 45 is written 32 x 5 and 60 is written 22 x 3 x 5.
Before looking at an efficient way to calculate HCFs we should look at these two numbers and factor each one out so that we can see the largest factor that is common to both of them.
45 = {1, 3, 5, 9, 15, 45}
60 = {1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60}
We see that there are more than one common factors to both but the largest that they have in common is 15. Armed with this clear evidence we take it back to the prime factor layout to see how and where 15 can be observed there.
15 = 32 x 5
60 = 22 x 3 x 5











