Mathematical Reasoning And Problem-Solving For All Primary Ages Using The Humble Triangle

Good things come in threes, says Mike Askew

- by Mike Askew
- Educator, researcher and speaker with a focus on primary maths education Visit website

This is the start of a new series of articles looking at aspects of mathematics that pupils appear to have found difficult in the national tests and unpacking why these aspects may be challenging.
My intent, however, is not to provide tips for ‘teaching to the test’ – far from it. Instead, I want to use challenging questions as a springboard for looking at how to make mathematics learning richer and deeper.
My jumping off point this month is a question on the KS2 reasoning paper that asked pupils to pick out one triangle from five that had an area different to the others. Only around 40% got this correct and it got me thinking about whether the study of triangles could go beyond the usual naming and describing to provide opportunities for problem solving and reasoning.
It’s not only buses that come in threes – there’s also wishes, bears and coins in a fountain, to name, well, three. I think there are sensible grounds for the fondness we seem to have for this number.
First is evidence from psychology that by about the age of, yes, three, children can, without counting, identify up to three objects in a collection – anything above that is just lots.
Second, from mathematics, three has a great stability: join three straws at the corners and the shape made cannot be pushed out of being ‘true’ the way that four joined straws can be. A three-legged table won’t wobble, unlike a four-legged one. No wonder photographers use tripods and novice cyclists are kept upright on tricycles.
And although our built environment, with all its vertical and horizontal lines, looks to be made up of quadrilaterals, behind those facades are a host of triangles. Naked, many structures would look like pylons. Simple and humble though it may be, the triangle may be a place to offer pupils some mathematical stability.
KS1 activities
KS1 pupils are expected to recognise and name triangles and describe properties of them.
Triangle sort ‘Recognise’ is one of the words that I would like to ban from the mathematics curriculum. For me, it is too passive as a verb – it suggests that we come to know something through frequent exposure to multiple examples of the same thing without the need to look at any underlying structure. I can come to recognise, say, the Eiffel Tower through seeing lots of images of it, but that will not help me understand any of the mathematics that holds it up.
The important thing in helping pupils ‘recognise’ triangles is that the typical examples of triangles that we present need to be introduced in an ‘example space’ that includes both non-examples and close examples chosen on the basis of what are the core features of ‘triangle-ness’: that is, three straight sides that are joined at the corners. Not four sides, not curved sides and no gaps at the corners (so that pesky instrument that the less musical pupils get relegated to play – I was one – should not be called a triangle at all).
Alongside this we also have to vary all the non-essential features of triangles – the angle of the base (why do textbooks present so many triangles with a horizontal base?), size, colour. A good example space for sorting triangles from non-triangles may look something like this:

Break and build Provide pupils with a stick of 12 interlocking cubes. Can they break their stick of cubes into three shorter sticks and make a triangle with those as the three sides (like this)?

How many different triangles can they make? Can they find a way to record them? How many triangles can they make with three equal sides, or two? Can they make a triangle with one side of six units? Can they explain why this cannot be done?
Lower KS2 activities
Pupils at this stage are expected to compare and classify triangles, identify acute and obtuse angles and know and use the names ‘isosceles’, ‘equilateral’, and ‘scalene’.
Nine-pin board If you can find them tucked away in the stock cupboard, physical nine-pin boards and elastic bands are ideal, otherwise present pupils with a sheet of a grid of nine-pin (3×3) boards. How many different triangles can they make on their boards?

Once pupils have generated a number of triangles, look at this either in a group, or, if you have a visualiser, with the whole class. How can you be certain two triangles are different?
Talk about the angles in the triangles, using the language of acute and obtuse to describe them. Can students make a triangle with one obtuse angle? With two? Talk about the sides of the triangles, using the language of isosceles, equilateral, scalene. Can pupils make two different isosceles triangles – one where the two equal sides are both longer than the third side and one where they are both shorter?
In the square Prepare for pairs of pupils a 3×3 square grid (each square being 5cm x 5cm). Label the grid as shown.
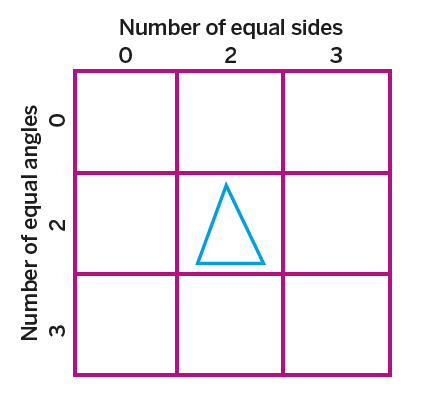
Working in pairs, can the learners create triangles to go in each square (they can draw these, or cut them out)? It will become clear that only three squares can be filled – along the diagonal from top left to bottom right. Discuss why the other six squares cannot be filled.
What can the learners say about triangles having equal sides and angles? Help them express their thinking in the form of conjectures in the form of “If… then …”, eg ‘If a triangle has two equal sides, then it has to have two equal angles.’
Upper KS2 activities
By the end of primary school, pupils are expected to be able to measure angles and calculate the areas of triangles. The following activities not only provide practice in these fluencies, but also the opportunity to reason about angle and area properties of triangles. Choose and construct Put the following collection of angles on the board: 30º, 45º, 60º, 80º, 90º, 110º, 125º. Ask pupils to draw a line 10cm long then choose two of the angle sizes listed on the board (they can use the same angle twice if they wish). They should then construct a triangle by measuring and making these angles at the ends of their line. They measure and record the third angle created. As a challenge, can they make a triangle with a right angle and an acute angle? Can they draw one with a right angle and an obtuse angle?
Between the lines Provide pupils with squared centimetre paper and ask them to draw two parallel lines two squares apart. Challenge pupils to draw, between the lines, as many triangles as they can, each with an area of 3cm2.
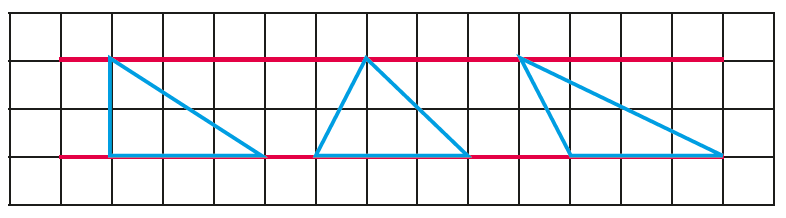
Once pupils have generated a number of triangles, look at this either in a group, or with the whole class. Invite pupils to explain how they know that the area of the triangle is 3cm2? Work on looking at the rectangles that just enclose their triangles and how the areas of these rectangles relate to the areas of the triangles.
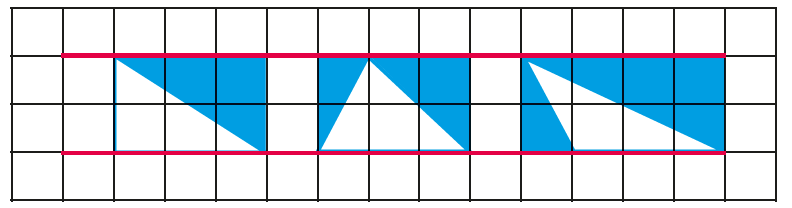
Introduce the idea of the ‘height’ of a triangle, and how in some triangles this sits outside the base of the triangles. How does the height of a triangle and the length of the base relate to the area of the triangle? (The area is half of the base multiplied by the height. Get learners to check if this holds true by drawing a different pair of parallel lines five squares apart and constructing triangles that sit between the two lines and checking the areas.
What’s in a name?
Upper KS2 pupils (and possibly even younger ones) may find it interesting to explore the origins of the names of the different types of triangles, rather than simply committing these to memory.
Our system for naming polygons (meaning ‘many-kneed’) is a mash-up of Greek and Latin and a bit of a mess in its lack of regularity.
We have a ‘tri-angle’ – a shape with three straight sides meeting at the corners – but the most regular of the triangles is named after the equivalence of its three sides, ‘equi-lateral’.
But, as the activity ‘In the square’ helps pupils come to appreciate, having three equal sides and three equal angles are dependent properties: given one, the other has to follow. The equilateral triangle could just as easily have been named the equiangular.
There is some consistency to the naming – ‘iso-sceles’ means two equal sides and ‘scalene’ means unequal (although the original Greek does not specify unequal sides, just unequal). The three names all draw attention to the properties of the sides of what perhaps should have been called the ‘trilateral’.
Mike Askew is adjunct professor of education at Monash University, Melbourne. A former primary teacher, he now researches, speaks and writes on teaching and learning mathematics. Find him at mikeaskew.net.










