Lowest Common Multiples and Highest Common Factor Needn’t be Boring – Creative Ways to Teach LCM and HCF

Multiply your possible approaches and factor in student access to make these subjects easier for them to comprehend

The topics of factors and multiples – leading from earlier work on understanding multiplication and division, partitioning, making systematic lists and arranging items in different ways – can sometimes feel a little stale to teach.
Once we start talking about highest common factor and lowest common multiples and referring to them using their familiar acronyms (HCF/LCM), you might feel as if there is no innovation to be had in this area at all.
So here are some ideas that you can use over a series of lessons, and over a flexible time period, that suits the needs of your particular class.
Conventional approaches generally fall under two categories: ‘make lists and compare’ or ‘Venn diagrams of prime factors’.
I have taught both and, since starting work at Cambridge Mathematics, realised that a more connected, thoughtful range of ideas on teaching these topics might have helped my teaching become not only fresher, but more conceptually effective – and that this topic is a really, really important one.
It’s one of the building blocks for so many other mathematical ideas: combinations and permutations; possibility spaces; factorising expressions and therefore solving equations; systematic error-checking and coding; max-min area and volume problems.
The connections are both delightful and somewhat intimidating – how can we teach students to both understand the concepts and become fluent in the processes, so that this topic isn’t a ‘bottleneck’ or barrier for later mathematics?
A good suggested place to start might be arranging objects in arrays, although if your students are secure in area calculations then accelerating ahead to them makes sense here – just be careful of cognitive load considerations.
Giving students cubes, sweets or other students to manipulate is useful; giving them a reason to do it is even better.
We need constraints of symmetry and equal sized rows and columns – so we could ask pupils to arrange 12 cubes in a block to simulate a bar of chocolate (uneaten!), 20 sweets in a pattern so that we could easily count them, or 24 classmates in rows so they can all see two sides of the classroom easily and we can move around the classroom if needed (a genuine real-life problem if ever I saw one).
It is important to be clear in the beginning that multiple solutions are possible and equally valid – and, in the spirit of play, that creative but possibly invalid solutions are also welcome for the questions they raise.
Moving from ‘find a solution’ to ‘find all the solutions’ is somewhere you could go at this point – then exploring which may be more useful or realistic and deciding how to effectively record those solutions is a good opportunity for pupils to exercise autonomy and/or teamwork.
As always, thinking about topics in terms of student access benefits everyone. How might we make sure a visually impaired student could access these ideas, for example? How might we ‘auralise’ an array so that pupils can hear it; how could we ‘feel’ for an array of shapes so that we can find the size of the rows and columns quickly and accurately? How about relating this concept to clapping patterns and bars of rhythm?
You may also be familiar with the game ‘Fizz Buzz’, in which the class individually recites the counting numbers and pupils take it turn to replace multiples of 3 and 5 with ‘Fizz’ and ‘Buzz’ respectively, leading to some ‘Fizz Buzz’ numbers.
You can ask pupils to articulate what happens, how often you say both words together and when the first time will be – before actually playing the game.
Making the link between the array of objects or the side length of the rectangle and its factors is an important conceptual point that shouldn’t be rushed. This example is taken from the Illustrative Maths curriculum, developed in the US, which is freely available under an open licence (although you will need a login):
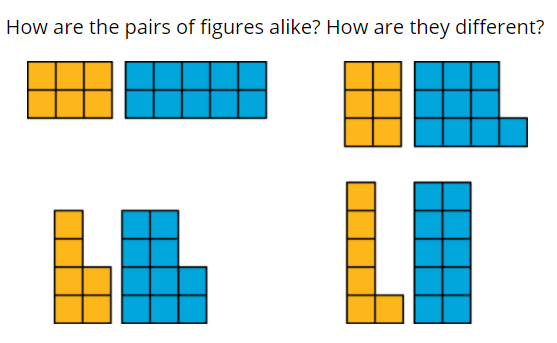
- 2 and 3 are both factors of 6. How is this reflected in the diagram?
- 2 is a factor of both 6 and 10. How is this reflected in the diagram?
- 4 is not a factor of either 6 or 10. How is this reflected in the diagram?
Notice how these questions invite pupils to use the diagrams to explain statements – an excellent introduction to a fast-paced section of the lesson where you can start to bring in some larger and larger numbers and encourage students to consider changing the type of representation.
It is also a great opportunity to start to invert the process and talk about multiples in a similar manner – “can I draw…?” and “why?”.
Lots of opportunity to continue to physically draw, for pupils that aren’t yet comfortable with the conceptual leap to abstract reasoning, will help support their thinking and using squared whiteboards might help avoid being bogged down with either rulers or mistakes.
Many other fruitful avenues are now open to you – depending on the age and fluency of your class, and your next preferred destination.
If you pursue ‘recording systematically’, you can consider lists of factors and scanning for common values – much of which could be beautifully linked to coding and algorithmic thinking (see Project Euler for some nice ideas on this).
If you decide to tackle Venn diagrams, the physical ‘making and breaking’ of cubes may lead nicely to ‘single cube towers’ and therefore primes.
You may like to pause at this point and delve into some lovely real-life problems like life cycles of cicadas, or consider sizes of teams put forward for sports day events among unevenly-sized classes (for something a little closer to home).
There is a fascinating nrich activity on cogs which could stimulate thinking about a different kind of representation here, and lead to some work on co-primes as an extension.
We’d love to hear your ideas and approaches to this topic, too – you can tweet us @CambridgeMaths.
Lucy Rycroft-Smith is research and communications officer for Cambridge Maths.











