How to teach developing maths reasoning in Primary

Teaching to develop reasoning in maths is a challenge. The solution lies in catalysing little and often, says Robert Wilne…

- by Robert Wilne

The 2014 National Curriculum introduced new topics and concepts into primary maths.
Naturally and rightly, a lot of professional development time has been focused on how to teach these to ensure that children develop confidence and fluency when ‘doing the maths’ – for example, when multiplying two proper fractions.
But the new curriculum also makes explicit the importance of developing children’s problem-solving and mathematical reasoning: each of these is as important as developing their fluency.
Many of the teachers I coach and develop, from NQT to SLT, have found that teaching to develop reasoning is hard to acquire.
This is understandable, not least because it wasn’t the experience many teachers today had when they themselves were learning maths in school.
Asking questions and designing tasks that lead to and encourage maths reasoning is often not an instinct; it has to be acquired.
A good first step towards developing your pupils’ reasoning is to ask: “Why is that your answer?” as often as possible, but this soon becomes very repetitive, for you and for the children.
Also, it leads to the belief that reasoning about a question or task comes after it has been finished, whereas reasoning can and should happen at every stage of exploring a mathematical problem.
So how can we get the children to explain ‘why’ without our having to ask it first? Consider these images: what’s the same and what’s different?
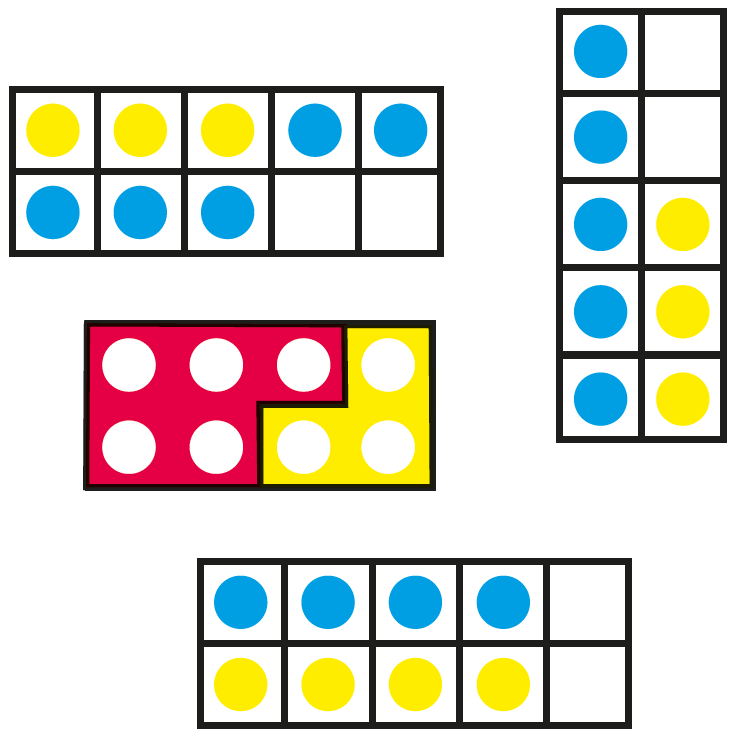
Many similarities and differences will occur to teachers:
- These are all representations of 8: three on tens frames and one using ‘number tiles’ such as Numicon.
- There are three representations that 5 + 3 = 8 (and related number sentences, eg 8 – 3 = 5 and 8 – 5 = 3) and one that 4 + 4, or double 4, = 8.
- Using the tens frames reminds us that 8 is 2 less than 10, ie that 8 + 2 = 10, 10 – 2 = 8 and 10 – 8 = 2
- The ‘vertical’ frame (top left), and to a lesser extent the number tiles representation, reinforce that 8 is ‘a whole 5, and 3 more’: I can show eight fingers with all five of the fingers on my left hand (the blue dots), no need to count them, and then three more (‘6, 7, 8’, the yellow dots) on my right hand. A ‘vertical’ frame looks more like hands, the dots being fingertips, than ‘horizontal’ frames do.
And what do KS1 pupils see? Many first notice the colours – “They’re all the same because they all have blue bits” – and some the orientation – “This one is going up and that’s different because these are going across”.
These are correct observations, and they are worthwhile because they include the word ‘because’, ie the children are justifying their observations – they are giving their reasons.
Practising reasoning using the properties of the images that are ‘surface level’ such as colour and position is worthwhile because it is preparation for reasoning about the mathematical properties of the representations, in particular the relationships they show between 3, 5 and 8 and 4, 4 and 8.
To draw these out, the teacher should keep asking, “What else is the same, what else is different?” and listen for responses such as, “They all have 8 dots altogether”, “There are three yellow and five blue dots”, “That one has the same number of blue and yellow dots”. These can then be pulled together.
The carefully chosen images create the opportunity for reasoning, and the questioning prompts the reasoning to happen: to adopt an idea from chemistry, the prompt catalyses the reasoning.
Of course, it may be that some or all of the children don’t articulate that the bottom representation shows a double and the others don’t, but that in itself is very useful for the teacher: if I’ve designed a lesson all about doubles and halves of numbers, but it seems that some or all children are not ‘seeing this’ in these initial images, then that tells me that I need to change my lesson design.
Assessment of their learning is also assessment for my teaching.
I now know I need to focus on representations of doubles. I can use another reasoning catalyst, with a different set of images.
Which might be the odd one out of:

This could lead to:
Pupil: There is a yellow ladybird, that’s the odd one out.
Teacher: Show me if you agree. Who now has a different suggestion?
Pupil: The bottom one only has five legs.
Teacher: Show me if you agree. Who chose another one?
Pupil: That one has more spots on one side, so it’s the odd one out.
Teacher: Can you explain what you mean?
Pupil: There are four spots and two spots.
Teacher: Thank you. Who chose another one?
Pupil: On that one the spots aren’t in a pattern.
Teacher: Can you explain?
Pupil: The other ladybirds have spots in lines.
Pupil: But still it’s 3 and 3. 3 and 3 is 6.
Pupil: 4 and 2 is also 6, but not like 3 and 3.
Teacher: Can you explain what you mean?
Pupil: 4 and 2 are not the same but 3 and 3 are.
Pupil: They’ve all got six spots.
Teacher: Let’s check that.
And so on: the teacher draws the mathematics out of the children. They come up with the idea of the total being the sum of the spots on each wing, and they notice that the total can be made in different ways.
Next, the teacher could ask the children to draw ladybirds with seven spots: “What’s the same and what’s different about 6 spots and 7 spots?” Once again, the questioning catalyses mathematical reasoning.
My recommendation, then, is to put reasoning activities, opportunities and prompts throughout every lesson. Reasoning can motivate the fluency practice, but it doesn’t have to follow it.
A lesson – a whole topic – can begin with a reasoning situation, and using a few familiar question prompts regularly will make reasoning happen increasingly quickly and deeply. Catalysing reasoning, like brushing teeth and eating vegetables, is best little and often, and it’s a lot more fun than either!
Robert Wilne is deputy director (maths) for Atlas Teaching School, and maths advisor for Bellevue Place Education Trust. He is also series co-editor of MathsBeat, OUP’s brand new primary maths programme.










