Division with remainders – Activities to combat maths misconceptions

Challenge children’s misconceptions about remainders through activities and questions that deepen conceptual understanding, says Beth Smith…

- by Beth Smith

Division with remainders has always been a concept that has absolutely stumped some of the children I have taught.
Over the years, I have had to consider different ways to combat this. Within this article, I will share some of these ideas and consider how they build upon each other to develop a deep understanding of division with remainders.
The first challenge when tackling division with remainders is the consideration of the two different structures of division. Children tend to be comfortable with division as sharing (partitive division). This comes from years of experience of sharing out food, pencils, stickers and so on.
Division by grouping (quotative division) tends to be a less familiar concept and therefore a harder one to visualise and understand.
I’m sure many teachers will have had the same experience as me at trying to explain how the method of short division works and had the baffled faces when you ask, ‘How many 3s are in 7?’
Some children try to revert back to sharing when dividing larger numbers and teachers despair at the image of circles and dots to try to solve divisions such as 75 divided by 5.
It is, therefore, vital that we use manipulatives to support the understanding of grouping so that we can help children to move towards abstract methods with a strong, conceptual understanding of why the method works.
When children are first introduced to remainders, lollipop sticks can be a good manipulative to use to represent what is happening.
Ask the children how many triangles they can make with 12 lollipop sticks, using one stick for each side. Investigate how many triangles we can make using different numbers of lollipop sticks.
Focus initially on multiples of 3, using stem sentences to make the clear link to division as grouping.

12 is divided into groups of 3.
There are 4 groups.
12 ÷ 3 = 4
Children can then move onto exploring numbers where there will be a remainder. By making the closed shape of a triangle, it is much clearer when there is a complete group and therefore which of the lollipop sticks represent the remainder.

13 is divided into groups of 3.
There are 4 groups with a remainder of 1.
13 ÷ 3 = 4 remainder 1
This activity also provides the perfect opportunity to address a common mistake that tends to appear when dividing using written methods. Anyone who has taught KS2 will have experienced something similar to the following:
18 ÷ 4 = 3 remainder 6
Here, the child has clearly made an error when counting in multiples of 4 and ended up with a remainder that is larger than the divisor (the number we are dividing by).
When we ask the children why it must be wrong, many children will check by attempting to resolve the division, possibly making the same error again.
Instead we need to support children to be able to spot that this must be wrong, due to the remainder.
Consider representing 18 ÷ 4 using the lollipop sticks.
If we look at 18 divided by 4 using manipulatives, we can see that, with a remainder of 6, we can make another group of 4.

18 ÷ 4 = 3 remainder 6
Children can then make their extra group of 4 and find the correct answer of 4 remainder 2.

18 ÷ 4 = 4 remainder 2
Leading on from this we can offer children the following proposal: ‘When dividing, the remainder can never be larger than the number you are dividing by.’
When creating proposals, or ‘I wonder’ statements, I have found a good way to support the children to engage with the proposal is to ask them to try to prove you wrong.
Here, children will find that we can always make another group if the remainder is larger than the divisor so therefore the statement must be true. This statement regarding remainders can be considered throughout KS2, just using different manipulatives.
It is important that this idea is returned to in each year to reinforce the idea of remainders despite the changing size of numbers.
Moving onto larger numbers, children can use place value counters to support them in their grouping.
Take this example from the White Rose Maths schemes of learning:
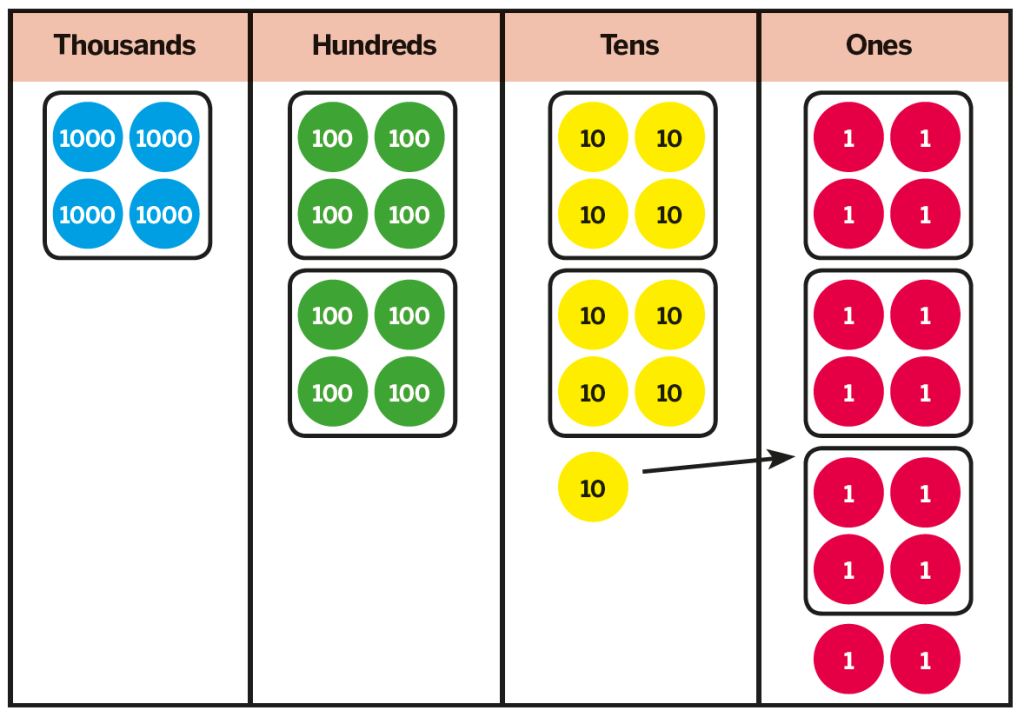
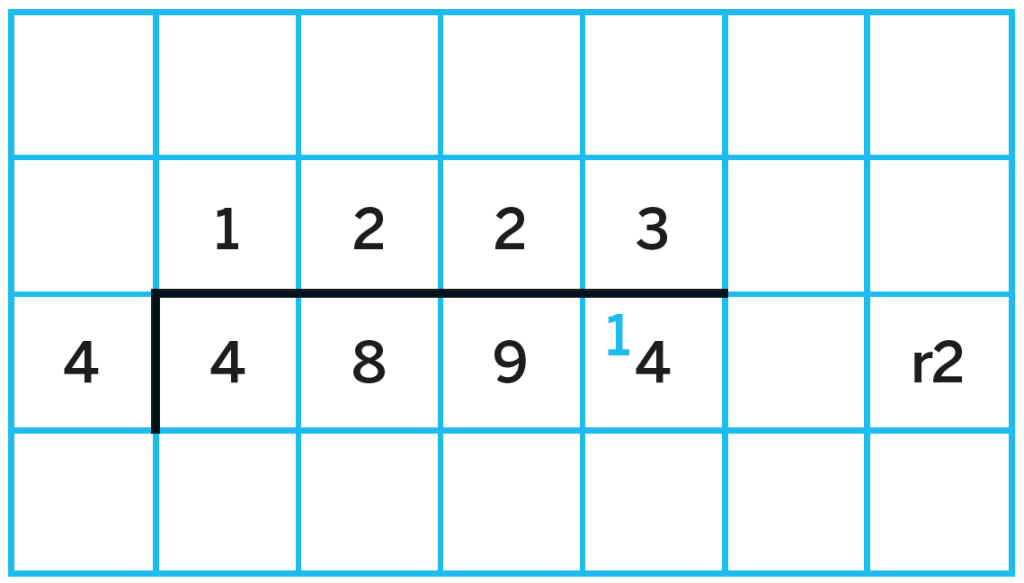
Here it is vital that teachers use the written short division method alongside the counters to support the understanding of how and why it works.
Since using the counters alongside the method, there have been so many light bulb moments in my classroom with children who have been baffled by the idea of ‘How many 4s are in 9?’ Now we can see what is happening and explain using precise vocabulary.
Notice, in the example above, the use of the exchange from the tens to the ones. Here we can see that the idea of a remainder now is applied in each place value column.
Applying the stem sentences that we used earlier, we can support conceptual understanding in the following way:
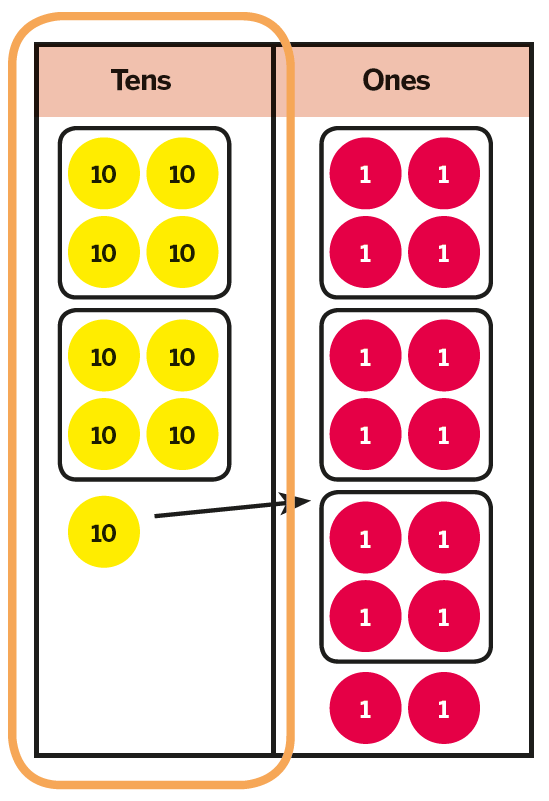
9 tens are divided into groups of 4 tens.
There are 2 groups of 4 tens with a remainder of 1 ten.
We exchange 1 ten for 10 ones.
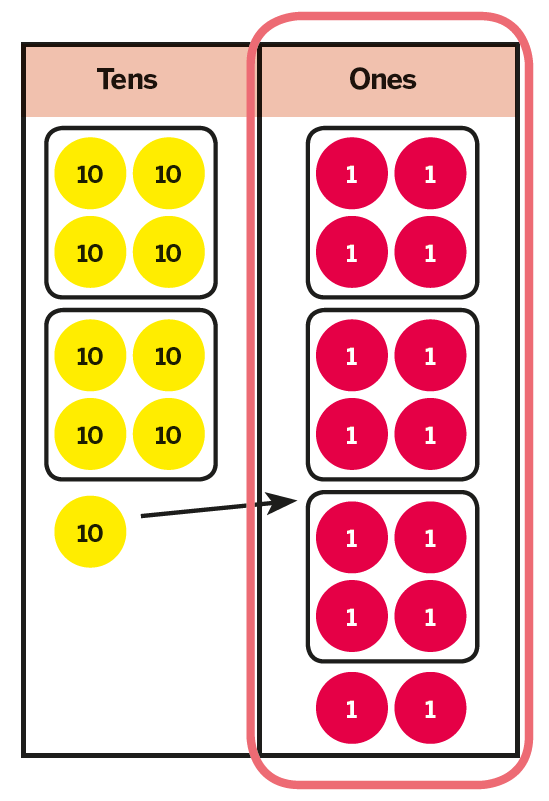
14 ones are divided into groups of 4 ones.
There are 3 groups of 4 ones with a remainder of 2 ones.
Here, there is a clear focus of the use of place value to reinforce understanding.
When teaching short division, some children try to describe the number in different ways – taking the example above they would say 90 ÷ 4.
Describing the division in this way doesn’t work as 90 divided by 4 would give a different answer to 9 tens divided into groups of 4 tens.
It is vital that children can see this difference so that they can understand the written method.
Moving into Y6, this method can be easily extended to consider exchanging the ones for tenths to give answers with up to 2 decimal places.
Once again, use the stem sentences to support deeper, conceptual understanding.
Finally, using carefully sequenced questions can support children’s understanding of remainders.
Look at this sequence of questions.

Here, we can see the use of variation to focus children’s thinking on remainders.
Having given a similar set of questions to both children and adults, during CPD sessions, it is amazing how many fall in to the trap of writing 215 remainder 4 as the answer to 648 ÷ 3.
This gives teachers the perfect moment to return to the proposal we considered earlier and to think about the size of the remainder.
Using the questions ‘what’s the same and what’s different’ encourages children to consider the numbers they are dividing and helps to highlight mathematical structures. Teachers can then support children in making generalisations that they can apply to other questions as well.
In this case, children might generalise about the divisibility rules of 3 and the idea that when dividing by 3, the highest remainder will be 2.
Through tackling maths misconceptions head on, teachers will find that topics that have been sticking points in learning won’t remain that way for much longer.
Beth Smith is senior primary maths specialist for White Rose Maths. Find out more at whiterosemaths.com and follow Beth on Twitter at @beth_89.










