Angles in the same segment – How to avoid confusion

Students are often unsure why angles in the same segment of a circle have to be equal. Colin Foster explains how to make it clear…

- by Colin Foster
- Reader in mathematics education at Loughborough University Visit website

In this ‘angles in the same segment’ lesson, students will explore the relationship between the angle at the circumference and the angle at the centre of a circle.
The difficulty
Anil says that the two angles shown in fig 1 below are equal. Do you agree? Why / why not?
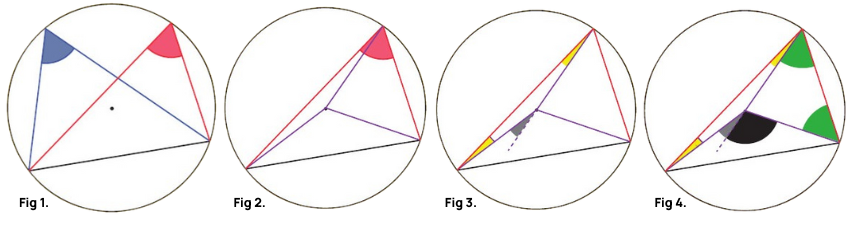
Students may agree with Anil by quoting the theorem that ‘the angles in the same segment are equal’. This is good application of a theorem, but they may struggle to explain why the theorem is true.
The solution
Let’s just think about the red triangle for now. A good strategy with circle problems is to draw in radii, which I’ve done in purple in fig 2. Now I’m going to colour some angles yellow (fig 3). What can you say about the yellow angles?
They are equal to each other, because they are the base angles in an isosceles triangle (the purple radii are all of equal length, because they are radii of the same circle). Also, the grey angle must be the sum of the yellow angles, because it is the exterior angle of the triangle that contains them.
Now let’s do the same thing with the green angles in fig 4. This time, the two equal green angles must add up to the black angle. This means that the grey and black angles together are equal to twice one yellow and one green. That shows that the angle at the centre is twice the angle at the circumference.
Checking for understanding
What would happen if you did the same thing for the blue triangle instead? Although the blue triangle is different from the red one, exactly the same process would lead to the blue angle also being half of the grey-and-black angle.
This means that the blue angle and the red angle must be equal to each other. And so must any angle in the same segment as them.
Colin Foster is a Reader in Mathematics Education in the Department of Mathematics Education at Loughborough University, and has written many books and articles for teachers. Find out more at foster77.co.uk










