Bar model – Explanation, resources and mistakes to avoid

From choosing the right model for each question to using the CPA approach, make sure your Singapore maths teaching is picture perfect…

- by Teachwire
- Classroom expertise and free resources for teachers

What is a bar model?
Independent primary maths consultant Cherri Moseley sets out the basics you need to know about bar models…
Put simply, a bar model is a way of illustrating a maths problem by using bars. When taught well, it can help to develop children’s understanding of maths, from basic number sense to high-level reasoning skills.
Where does Singapore come into it?
During the 1960s and 70s, children in Singapore were doing very poorly in maths, and were certainly not appearing at the top of any international comparison tables. They were taught tedious calculations using learned procedures and memorised facts, without understanding what they were doing or why it worked.
So, the methodology was changed to the Concrete-Pictorial-Abstract approach (CPA), or as Anne Watson, Emeritus Professor at the University of Oxford would say, doing it with ‘stuff’.
CPA approach
It doesn’t matter what that stuff is – just start with real objects, move on to counters, cubes and other representations (including drawings), before progressing to the abstract written form.
Mathematical problems always contain knowns and unknowns. There will always be some kind of relationship between the parts and the whole. If there wasn’t, we would not be able to work out one from the other.
The bar model, the most recognised feature of the Singapore mathematics curriculum, illustrates this relationship. It does not do the mathematics for you, but highlights what you know and what you don’t know. In other words, it shines a light on the problem.
There are two main types of bar models – the part-whole model and the comparison model.
The part-whole model
Concrete
You might set children a problem such as: ‘There are 5 green apples and 3 red apples in the bag. How many apples in the bag?’.
With younger children, use a bag of apples. Get the apples out of the bag, sort them into green ones and red ones, then put them into a line to help children count them. You are putting the parts together to find the whole.

Setting out objects in a row makes them easier to count and you can already see the beginnings of a bar. The next step in the development of the approach is to model the problem using something else to represent the apples.
Although you are still being concrete, you are using a generic representation. We could be thinking about five and three of anything.
Pictorial
The next step is to start drawing, still using a one-to-one representation. You could draw apples, but children soon realise this is time-consuming and are usually happy to use a square, cross or something else to represent each apple.

Soon, you can move on to using a proportional bar rather than a one-to-one representation. Children in Year 2 quickly get the idea, and older children even more rapidly.
You draw one bar to represent the whole. Early problems will likely include two parts, so you draw another two bars that together are the same size as the whole.
Later, there will be more parts and you will need to change your drawing accordingly. In some problems, it might be useful to draw more bars to help children see their way into the problem and how to solve it.
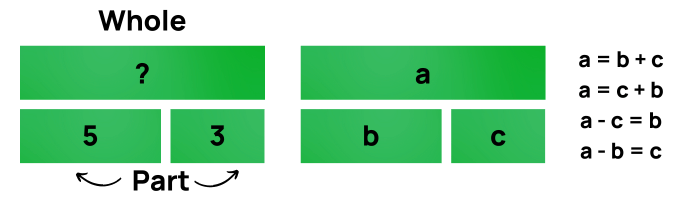
So, this is our basic model. Provided we know any two values, we can work out the third. The bars are labelled a, b and c here for clarity.
Children will label the parts that they know and put a question mark in for what they don’t know. You can see how this can lead on to algebra in due course.
Comparison model
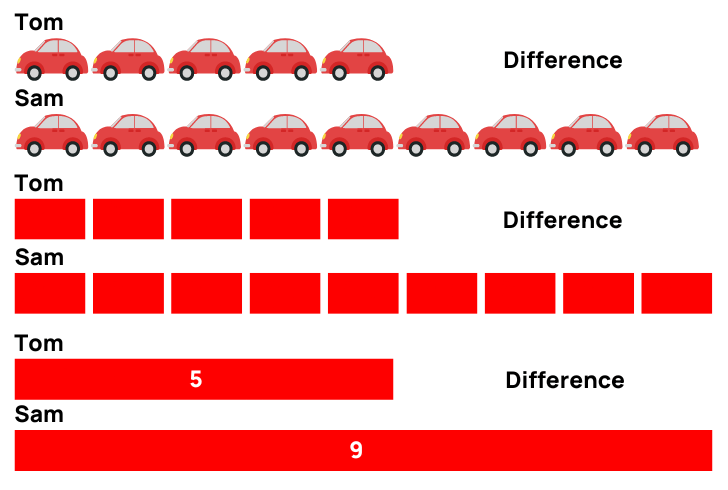
This model helps you compare two quantities. Again, start by lining up real objects before moving on to counters or cubes, then a bar. Here’s an example of a problem that you could use the comparison model to solve.
Tom is playing with 5 toy cars, Sam is playing with 9 toy cars. How many more cars than Tom does Sam have?
Sam has 4 more cars than Tom. As the model is developed, you can represent the same problem using blocks, and then drawing it.
Free bar model resources
Bar model worksheets and CPD
These free bar modelling maths resources from White Rose Education are perfect for primary or secondary pupils. All the worksheets come with answers to make marking easy. There’s also a PowerPoint presentation which forms the basis for a one-hour CPD session for staff.
Bar model maths lesson plan

This bar model maths lesson plan from Cherri Moseley features a number of bar model maths problems for children to solve. The first set of problems use the part-whole model, while the second set focuses on the comparison model.
Bar model teaching mistakes to avoid
Mohi Uddin Ahmed from The Bar Model Company sets out some common mistakes teachers make when teaching bar models, and what to do about them…
There are a few things to consider before implementing a bar model approach in your school. I visit lots of schools that are introducing the approach in their settings and have noticed a number of common mistakes.
This means that after the initial excitement and eagerness to reveal a fantastic strategy to your staff and children, it can quickly feel like an uphill task.
So, what are these mistakes, and how do you get past them? Let’s take a look.
1 | Not fully using the CPA approach
Not fully using the CPA approach is the first major mistake when introducing bar models. Why does this happen? Well, you may have seen bar models online and in books, but that may mean you’ve only seen them as pictorial representations.
When introducing bar models to your pupils it’s imperative that you follow Jerome Bruner’s Concrete Pictorial Abstract (CPA) approach.
This means that it’s important for teachers and children to use concrete materials for bars when attempting to use this strategy to solve problems.
There are commercial products available, which has meant some teachers using the bar model approach are also using concrete materials when modelling some questions, but are they doing it consistently?
“It’s important for teachers and children to use concrete materials for bars”
Ask yourself:
- Are you consistently using concrete materials?
- Are you letting your pupils use concrete materials?
- How can you consistently use concrete materials?
- When should you let your pupils move to pictorial representations?
- Is there a transition technique that allows your pupils to smoothly and accurately understand and draw bar models?
If your school doesn’t use the CPA approach consistently, it’s likely that pupils will not understand the key elements of the bar model approach. This means they will not be able to generalise, and therefore master, the approach.
2 | Forgetting about consistency
We always aim for consistency in what we say and do in our schools, but when it comes to bar models, many schools forget about consistency. Why? Well, it might be because bar models all look the same – like bars, right?
So as long as all teachers are drawing bars it should all be consistent, surely? Wrong! So what do we mean by consistency? Have a look at the picture below.
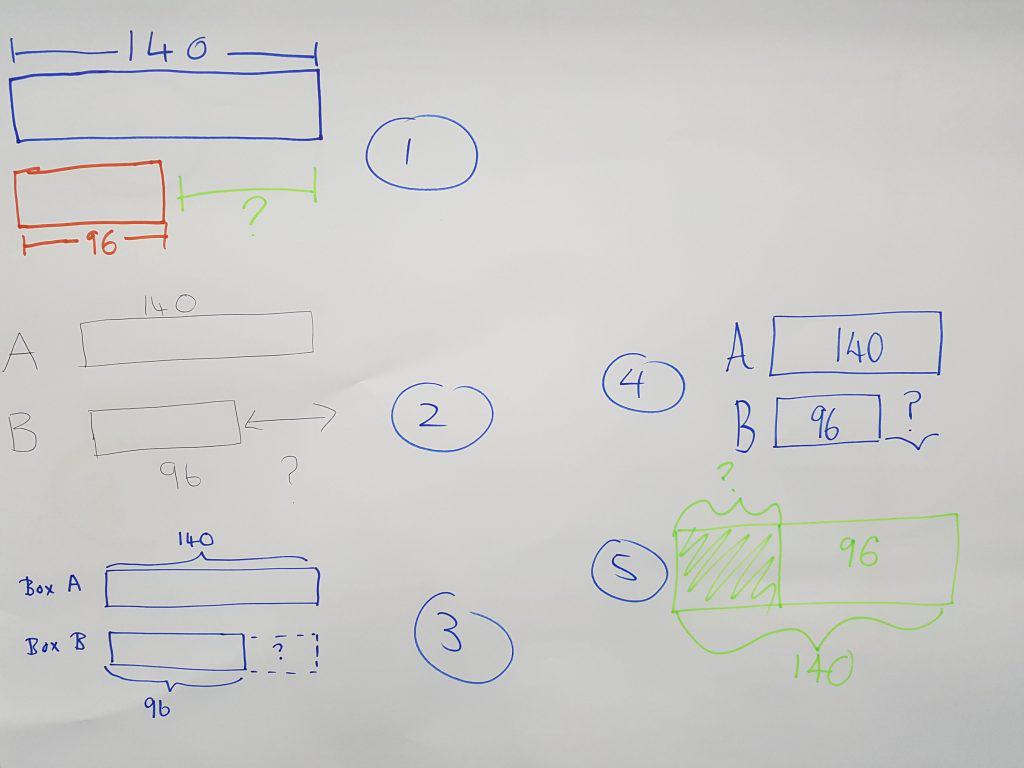
It shows different solutions in a seminar with a group of delegates from over ten schools. They came up with various different ways to draw the Singapore model solution for one question.
The actual question was a very simple subtraction question. Yet even for one of the most simple model questions we had various different solutions offered to us. This happens in every training session we deliver.
Ask yourself this:
- Should teachers draw bar models how they think is best?
- Is that a good whole-school approach?
- Is there a problem with allowing teachers that freedom?
- What should you do?
A consistent approach will always result in a more efficient use of bar models throughout your school. It will also lead to fewer pupils being confused and fewer mistakes from both teachers and pupils.
So there is a need to be consistent. But what is the best approach from the above pictures? Is there a better option than the ones the teachers have suggested above? What would the National Institute of Education subscribe in Singapore?
“A consistent approach will always result in a more efficient use of bar models throughout your school”
Here are some more points to consider before you start to introduce bar models to your school:
- Are we training teachers in the same way?
- Is there room for flexibility?
- If so, what would that look like?
3 | Lack of focus on the basics
In many schools, there is a lack of focus on the two core bar models:
- Part-Whole
- Comparison
At Upper KS2 level, where many schools are using Singapore maths textbooks, teachers have jumped into the top end of the model questions even though the schemes rely on pupils having experience in using the model in the previous years of primary education.
As pupils don’t have this experience, many are not too sure about bar models. We’ve forgotten to go through the basic concept of part-whole and comparison models.
Even within these models, there are core foundations which we have to carefully teach through high-end questioning and visual modelling to get the most out of the model approach.
An example of a part-whole model
4 | Neglecting Early Years
Before formal approaches to bar modelling kick in around Year 2, many schools are not sure how to support EY and Year 1 teachers. In fact, a common gripe amongst EY teachers is that they feel left out in almost every CPD in which their school invests.
The use of ten-frames and number bond diagrams (also known as part-whole diagrams) are a prerequisite of bar modelling. However, many schools jump into teaching bar modelling without this foundation.
The use of games such as trump cards is a very useful and engaging way of using bar models at a young age. In fact, the use of the model in the trump cards is very subtle as it just feels like playing a game.
5 | Choosing inappropriate models
When things are not going well in a lesson using bar models, pupils might blame the model approach for their failure to solve a question. In many of these incidents, it is a failure to understand basic models and also choose the appropriate model.
When do I use the part-whole model? Should I use the comparison model? How do I know which one to use? This is the first issue many pupils will face.
6 | Lack of experience
This is two-fold – from a teacher’s point of view, and also from a pupil’s. Many schools jump into the textbooks without thinking about the lack of experience children have in using the model approach.
But equally as devastating, in some schools, is the lack of experience teachers have. They feel they have been flung into the high-end bar model questions, meaning they sink rather than swim.
“Many schools jump into the textbooks without thinking about the lack of experience children have”
How can we prepare pupils for high-end questions before we get to those chapters? How do we allow teachers to build their own confidence? Should we just let them dive in whenever they come to a chapter on bar models?
7 | Weak questioning skills
We know from the research done by Zoltan Dienes and Jerome Bruner that using the CPA approach (Bruner) and constructively-active learning (Dienes) is an effective way of teaching.
What Zoltan Dienes goes on to say is that the mere use of concrete materials is not enough. Our questioning and modelling has to be strong.
So, can we question the children to edge their thinking forward so that by the end of a question they feel they are the ones that solved the problem?
Or are we giving too much away, so that when we do let go our pupils still seem lost, and like they are not making as much progress?
8 | Low engagement
It can be tricky to maintain high rates of engagement in maths lessons sometimes. One way is to use animated videos to engage your pupils and make bar modelling less daunting and much more accessible.
Mohi Uddin Ahmed is a Singapore maths consultant and trainer for The Bar Model Company.










