4 KS3/4 Maths Problems to Help Teach Highest Common Factor (HCF) and Lowest Common Multiple (LCM)
Play Product Sudoku and revel in Robotic Rotations to help your pupils get to grips with factors and multiples in a fun and engaging way

- by Ems Lord

In this article, the NRICH team share four of their favourite activities for developing a greater understanding of HCFs and LCMs. Each activity encourages your students to work mathematically, justifying their solutions and considering alternative approaches to problems.
Getting started on a problem is often a challenge itself. At NRICH we find that students who get stuck often find it helpful to explore other students’ starting points then continue that solution, so we aim to feature student solutions to all of our problems on the website.
1. Gabriel’s problem
Here’s an example showing how that approach might look in the classroom using Gabriel’s Problem (nrich.maths.org/Gabriel’sProblem).

Let’s consider one of the student solutions for Gabriel’s Problem.
Alice focused her attention on what she knew, rather than what she did not know.
Sharing part of her solution with your students can enable them to get started on the problem themselves.
Alice began by looking at the multiples, searching for those with the fewest factors. She recognised the prime number 21 and reflected on her knowledge of primes, “The product of the middle column is 21, which is only divisible by 1, 3 and 7. Therefore the numbers in the middle column had to be 1, 3 and 7.”
From that successful starting point, Alice adopted a similar approach towards the multiples of 10 when she noticed, “The product of the left column and the middle row are multiples of 10 therefore they had to have 5 as one of their numbers. The only square they share is the middle square of the left column so that is where I put the 5.”
Alice just needed to complete the remaining factors to reach her solution, “Because 24 is not divisible by 7, I put 7 in the middle of the bottom row, leaving the 3 in the middle of the top row. I then turned my attention to the middle row and calculated that 1 x 5 = 5 and 5 x 8 = 40, so I put the eight in the right-hand square of the middle row… 9 was in the right-hand square of the bottom row because the products of the right-hand column and bottom row were high.”
Once students have understood her approach, there are several more similar puzzles on the same page which they can solve by applying their new skills.
2. Using puzzles
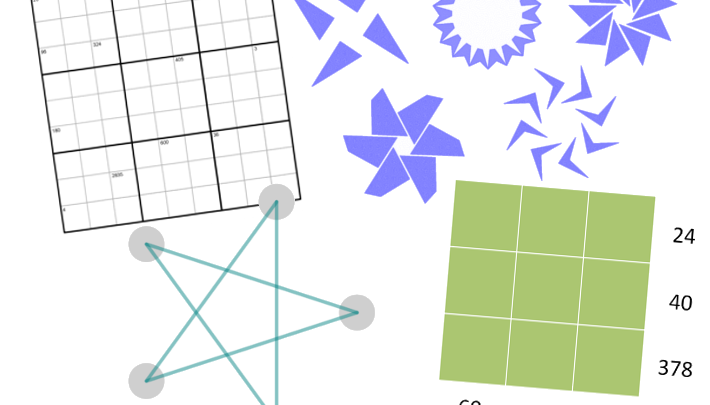
Using solutions is one effective approach. Another one involves engaging students through puzzles. Sudoku must be one of the most popular formats. The NRICH team have devised a special version focusing on HCFs and LCFS which we’ve called Product Sudoku.
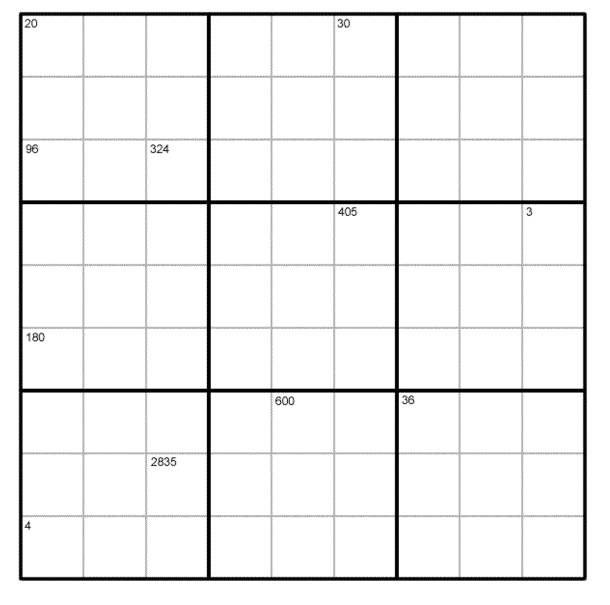
The rules for Product Sudoku will seem very familiar to fans of the more conventional version of the puzzle:
- Each column, row and 3×3 subgrid must have the numbers 1 to 9
- No column, row or subgrid can have two cells with the same number
The puzzle can be solved with the help of the numbers in the top parts of certain cells. These numbers are the products of the digits in all the cells horizontally and vertically adjacent to the cell.
A helpful way to get your students started on the puzzle is asking them what they notice about some of the cells. Several of them have numbers in their corners.
The cell in the top left corner of this Sudoku contains the number 20. So 20 is the product of the digits in the two adjacent cells, which therefore must contain the digits 4 and 5.
The 5 cannot go in the cell below the top left hand corner because 5 is not a factor of 96 (the product shown in the third cell down on the left hand side of the puzzle).
Therefore 5 must be entered into the cell to the right of the cell containing 20 and 4 in the cell below. Working in a similar way with the other cells will lead your students to a solution.
Once they have mastered the puzzle, perhaps they might like to explore our more-challenging version called Diagonal Puzzle Sudoku.
3. Stars
Our third problem encourages students to see the mathematics underpinning a situation. At first glance, it is a geometrical setting but it is understanding the importance of factors and multiples that will guide them to a solution for Stars.
Indeed, to avoid spoiling the surprise, it may be worth doing this activity at the start of work on the topic, without telling the students what the topic is…
Begin by asking them to draw a five-pointed star starting and ending at one of the “points” or vertices of the star. They must do this without taking their pencil off the paper and without drawing over a line they have already drawn. Many students will have met this before.
Then ask the group to discuss in pairs a description of what they did that they can share with the rest of the group. “How would you explain to someone else, at the other end of a phone, how to draw the star?” Look out for ideas such as step size and ways to describe positions.
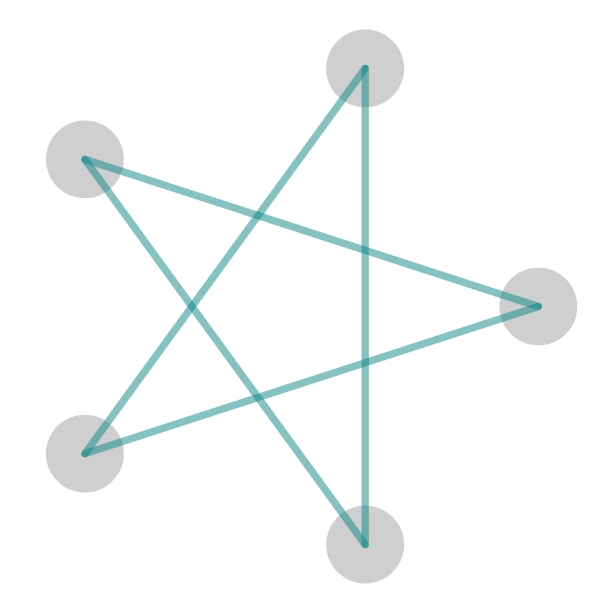
Example of a five-pointed star
When your students are ready, demonstrate a five-pointed star either using an interactivity or by getting a group of students to stand in a circle and make the stars with string (by passing a ball of string).
Discuss the notation that has been used (going anticlockwise, stepping by two leaves two gaps between the points on the circle), and discuss points of interest including:
- What happens if you move clockwise?
- What constitutes a star (in these notes a polygon created from a step size of 1 is not a star)?
- There is only one star on a five-dot circle.
- Complementary step sizes produce the same star (step size two is equivalent to step size three in this five-dot context)
Ask your students to make as many stars as possible on a seven-dot circle:
- How many stars can they make?
- How do they know they have them all?
Challenge them to conjecture how many stars will be possible on a nine-dot circle (without drawing them at this stage). Discuss in pairs before sharing what they can offer as a convincing argument.
Your students can now focus on generalising their results for any dot-circle. If working with a small group – ask each person to create a star based on a different step size and compare the group’s results, encouraging the students to identify what is the same and what is different about their stars and putting them into an order they can justify.
Encourage individuals to draw a star and, without showing it to their partner, give instructions to draw the same star. Are the two stars the same? The activity could be carried out using string on peg boards.
4. Robotic rotations
Our final activity appears at first to be about angles and rotations but, as your students explore more deeply, they may be surprised to discover links to factors, multiples and primes.
The images for Robotic Rotations provide an enticing hook to stimulate students’ curiosity:

Examples of patterns for discussion
What do they notice about the pictures? What’s the same, what’s different about them?
It might be a good idea to encourage them work out the rotational symmetry of each image. For example, figure 5 (below) has rotational symmetry of order 4. That means there are four copies in a full 360 degree turn. So each rotation must be…

Example of rotational symmetry
This knowledge allows your students to explain how the image was produced as well as enabling to explain the other images too.
Then you can draw their attention to the last part of the task: can they find a link between the angle and the number of copies of the image in the pattern?
Allow some thinking time and then explain that you will create a shape and choose an angle, expecting them to be able to predict how many copies of the shape will appear.
In the final plenary, you could challenge them with a few angles and ask them to predict and explain how many copies there will be and expose the links to HCFs and LCMs.
For example, for 160 degrees there will be nine copies, because the highest common factor of 160 and 360 is 40, and 40 goes into 360 nine times.
Ems Lord, is the director of NRICH. The NRICH team hope that your students enjoy this set of rich mathematics puzzles focusing on HCFs and LCMs. We offer free curriculum maps to help make every day a problem-solving day in your classrooms.
Every half term, we publish a new set of free resources and we welcome student solutions to those Live Problems. We’ll even publish some of the best ones too.










