Students can often become confused over how to round a number to a specified number of significant figures. Use this free worksheet to help them avoid getting in a muddle with zeroes and columns when rounding numbers.
Rounding numbers lesson
In this lesson, students connect significant figures to other ways of rounding. The first task involves filling in the missing numbers in the table below:
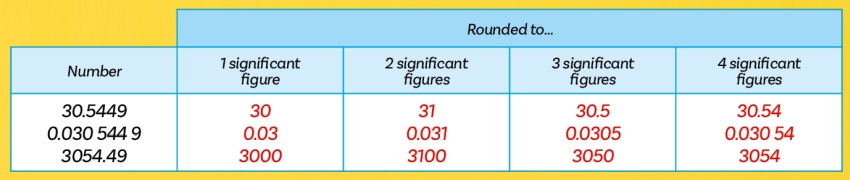
Students may be confused about what ‘significant figures’ means and round to 1, 2 and 3 decimal places instead. Or they may be confused about whether to count zeroes or not. This means they might think that 30.5449 to 2 significant figures is 30.5.
Or they may use incorrect ‘successive’ rounding when working out 30.5449 to 4 significant figures, rounding 30.5449 first to 30.545 and then rounding this rounded value to 30.55.
The solution
For each of these numbers, say which column the most significant digit is in.
30.5449
0.030 544 9
3054.49
5.3449
0.53994
534.99
This can be a quickfire activity, with flashcards and mini whiteboards. Each time, all students need to do is identify the column (ones, tens, tenths, thousandths, etc.) containing the digit worth the most.
It will always be the first non-zero column from the left. Students might incorrectly think that it is the largest digit – e.g., the 9 in 30.5449. However, this is actually worth the least.
Rounding numbers to one significant figure
To round to 1 significant figure, we round to this column. So, to round 30.5449 to 1 significant figure, we round to the nearest 10. To round 0.0305449 to 1 significant figure, we round to the nearest 0.01. To round 3054.49 to 1 significant figure, we round to the nearest 1000.
Write down 10 more statements like these, making the numbers as varied as you can.
Allow students to abbreviate their sentences to avoid repetition, or you can just ask them to list the two numbers for each statement. Alternatively, use the printable ‘Significant figures’ worksheet above.
Rounding numbers to two significant figures
Now look at what happens for 2 significant figures. To round 30.5449 to 2 significant figures, we round to the nearest 1. To round 0.0305449 to 2 significant figures, we round to the nearest 0.001. To round 3054.49 to 2 significant figures, we round to the nearest 100.
You might need to remind students that ‘rounding to the nearest 0.1’ or ‘rounding to the nearest tenth’ is the same as ‘rounding to 1 decimal place’.
Write 10 more statements like these, again varying the numbers and using several different numbers of significant figures.
Now complete the table below. The answers are included here in red – find a blank version in the download above.
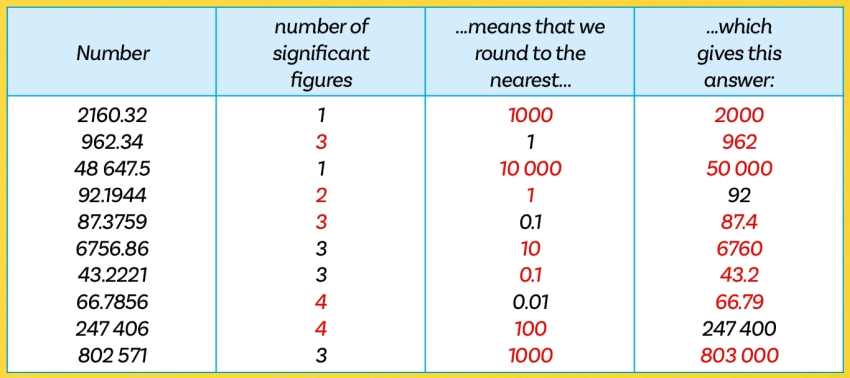
Here, we have the number 247 406. Why would it be a problem if we change that number to 247 401?
This may be hard for students to answer, but the transformation 247 406 → 247 400 must be rounding to the nearest 100. However, 247 401 → 247 400 could be rounding to the nearest 100 or the nearest 10, leaving two possible answers.
Checking for understanding
To assess students’ understanding of rounding numbers, ask them to create a table like the one above for their partner. Swap, complete, and then swap back and check.
Colin Foster (@colinfoster77) is a Reader in Mathematics Education in the Department of Mathematics Education at Loughborough University and has written numerous books and articles for mathematics teachers. For more information, visit foster77.co.uk














