Area and perimeter – Best worksheets and ideas for KS1/2 maths

Help primary children know their shapes inside and out with these geometry teaching resources for area and perimeter…

- by Teachwire

Unlock the secrets of shapes with our curated collection of engaging area and perimeter worksheets and creative teaching ideas for Key Stage 1 and 2 students…
Area and perimeter resources
Area and perimeter activity cards
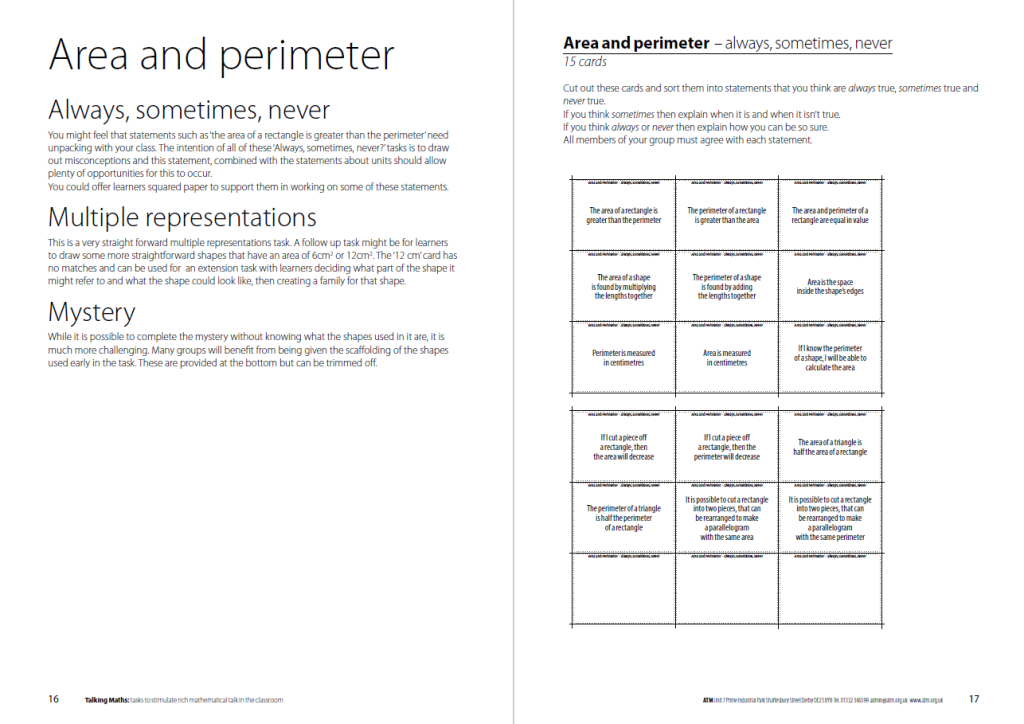
This area and perimeter activity cards resource from the ATM comes from its Talking Maths series, and includes an introduction sheet for teachers and three area and perimeter activity cards:
- Sort the cards into statements that you think are always true, sometimes true, never true
- Match cards that show different ways of representing the same shape
- Problem-solving card activity
Area and perimeter guide and free printable worksheet

This page includes a brief guide to give upper KS2 students an overview of area and perimeter, and you can download a 14-page PDF worksheet and separate answer sheet too.
The questions have been stripped from past papers, so it should give pupils an idea of what might come up in SATs.
Perimeter and area of rectangles
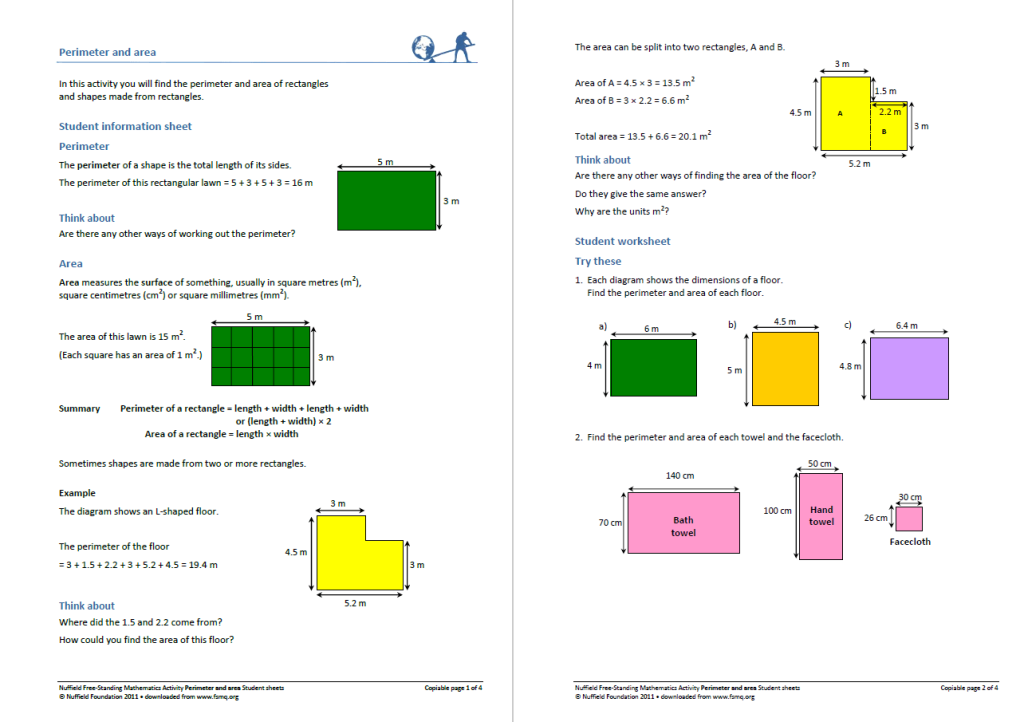
In this activity from the Nuffield Foundation, children will find the perimeter and area of rectangles and shapes made from rectangles.
KS2 area and perimeter medium-term plan

Here’s a medium-term plan on area and perimeter from Piximaths. There are four sections:
- Introduction to area and perimeter
- Area and perimeter using formulae
- Area and circumference of circles
- Arcs and sectors
NRICH area and perimeter
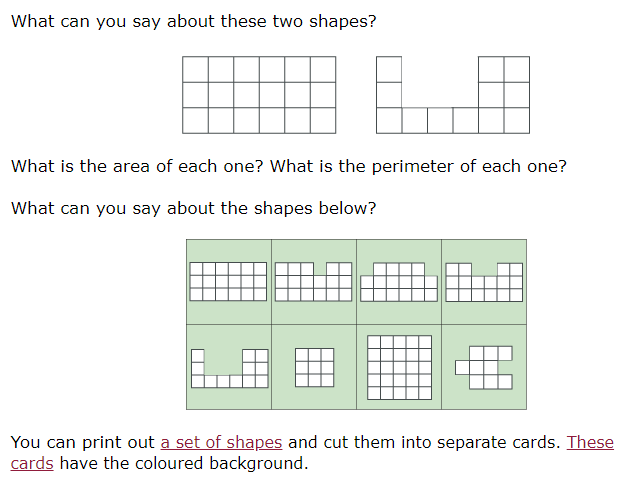
This NRICH article (which comes with printable resources too) has a range of fun challenges that’ll get KS2 students exploring the relationship between area and perimeter for themselves.
It tasks them with things like:
- Drawing a shape where the area and perimeter are the same
- Drawing one where the perimeter is numerically twice the area (and vice versa)
- Making the area of a shape go up while the perimeter goes down
- Drawing shapes that have the same area but different perimeters
Area worksheets and resources
Area worksheet pack – Area of rectilinear squares

These area worksheets from Plazoom provide extra challenge for Year 4 children by getting them to find the area of rectilinear shapes by counting squares.
There are a variety of area problems spread across three sections, enabling you to use the whole sheet during a lesson or to select specific problems for different teaching sessions. Separate answer sheets are included for all sections.
Calculating area of a rectangle worksheet pack

Carrying on with this scheme, these Year 5 worksheets ask students to calculate and compare the area of rectangles (including squares), including using standard units, square centimetres and square metres. They also have to estimate the area of irregular shapes.
As with the Year 4 sheets, there are three sections, all with answers. Just be sure to print them at 100% for the measurements to be accurate.
Right-angled triangles free printable worksheet
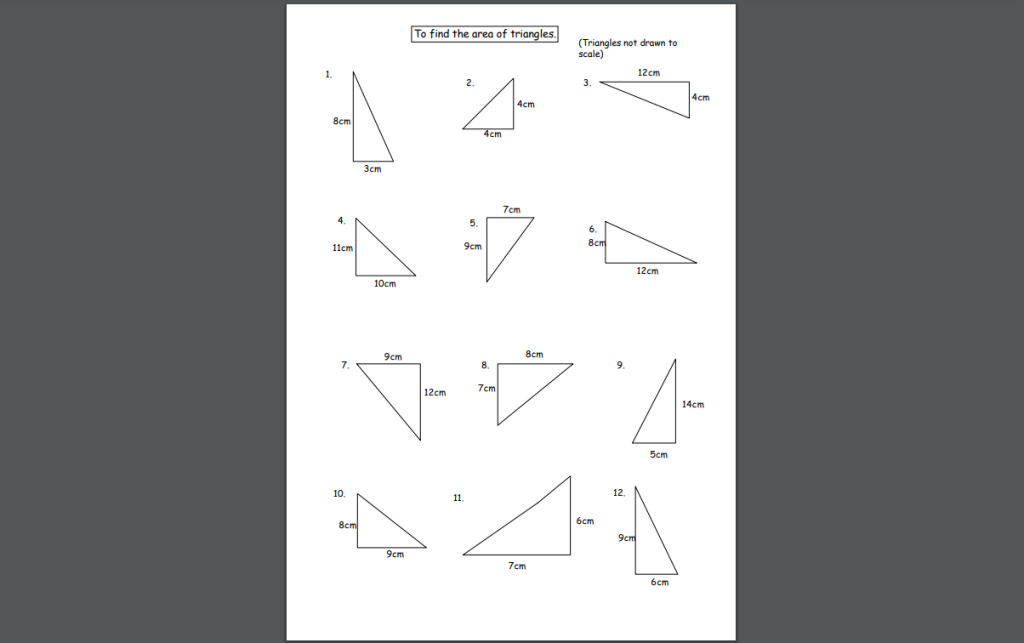
If you want to test your students on their newfound triangle skills, this simple geometry worksheet features 12 questions asking them to find the area of right-angled triangles.
Perimeter worksheets and resources
Using real-life examples to teach perimeter

Challenging pupils to apply knowledge in a practical way is fun and will help them retain essential information. The activities in this free KS2 lesson plan can be easily adapted to add further challenge or support.
Perimeter for Years 3-5
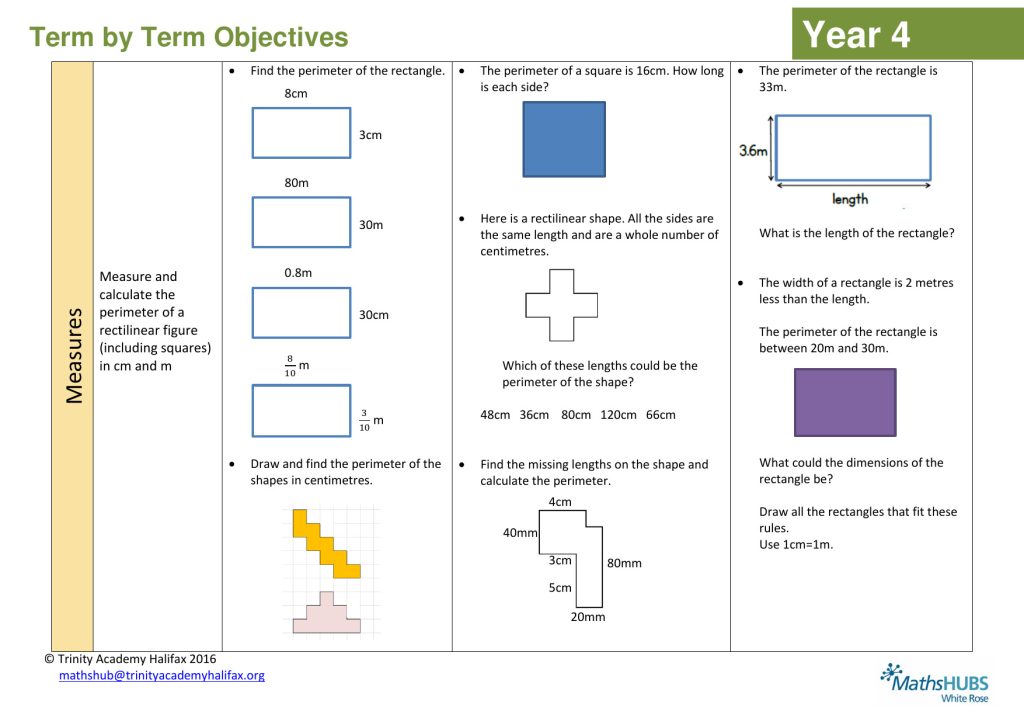
The White Rose Maths Hub is funded by the government and works with hundreds of primary schools. Download its scheme of learning for perimeter for Y3, Y4 and Y5.
- The Y3 resource covers calculating the perimeters of 2-D shapes in centimetres or millimetres.
- The Y4 resource covers measuring and calculating the perimeter of a rectilinear figure.
- The Y5 resource covers calculating the perimeter of composite rectilinear shapes.
Perimeters – Y3 measurement maths challenge

These perimeter review worksheets from Plazoom provide extra challenge for Year 3 children. They feature a variety of perimeter problems are spread across three sections, enabling you to use the whole sheet during a lesson or to select specific problems for different teaching sessions.
A separate answer sheet for all sections is included.
Perimeter worksheet for more complex shapes
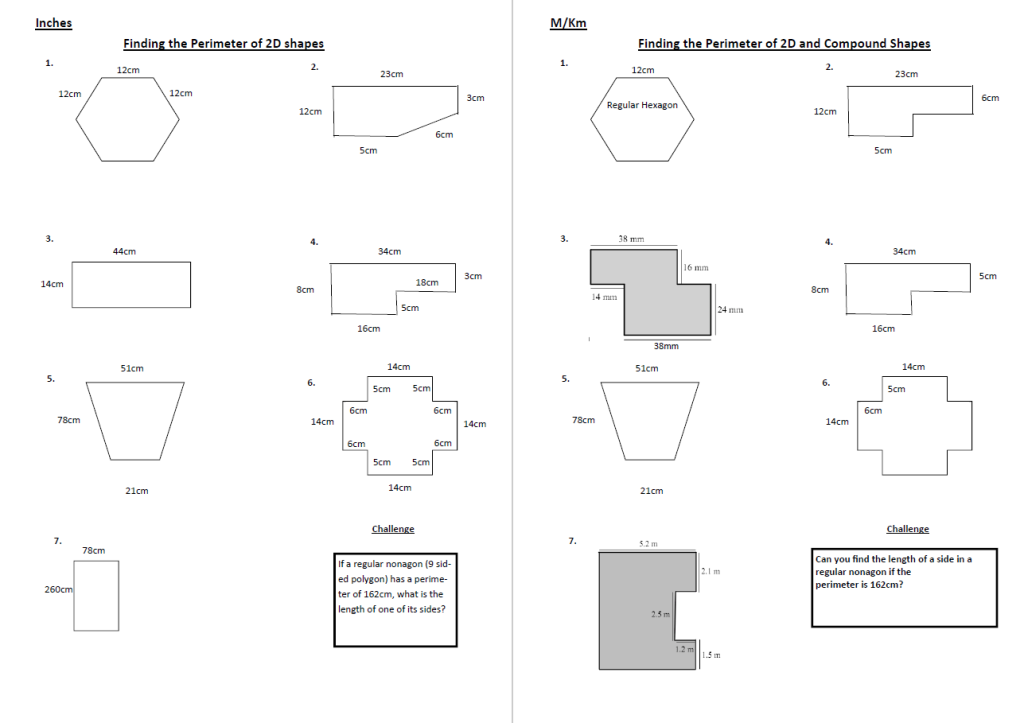
This worksheet is separated into four sections, each of which features seven questions and a challenge.
The sections are:
- Rectangles and squares in mm
- 2D shapes in cm
- 2D shapes in inches
- Compound shapes in mm, cm or m
Interactive tools and games
Perimeter explorer
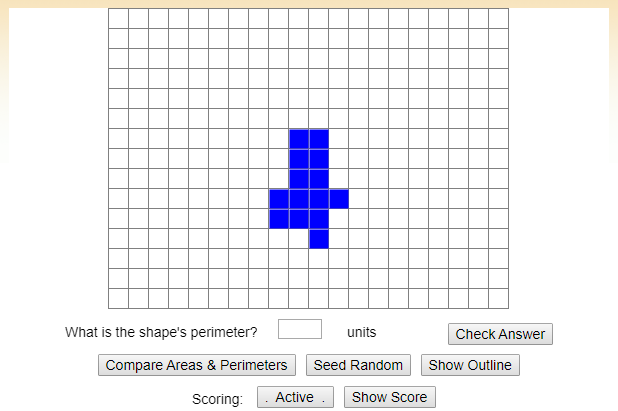
This handy interactive tool creates random shapes and asks students to work out the perimeter. Just type in your answer and hit the ‘Check’ button to see if you’ve got it right.
You can choose the number of squares in the shapes, from 1 to 46, and there’s an option to only create rectangular shapes too.
Perim-bots

Here’s a great little game that challenges you to answer six perimeter questions, and collect a robot part for each correct one.
You get to choose from a selection of heads, bodies, arms and legs to build your robot, and the variety of questions keeps things interesting too.
Real-world perimeter measuring activities for LKS2

Get your ruler and string at the ready and try these real-world measuring activities for LKS2 from teacher Lydia Davison…
When we consider perimeter, it is not uncommon to envisage a collection of 2D, not-to-scale rectangles pre-drawn on a worksheet for children to calculate the total length of sides.
Fast forward to assessment or retrieval practice and pupils, pencil in hand, have a 50/50 chance of success – dictated by a toss-up on whether to multiply the sides or add (the infamous area vs perimeter confusion).
At its core, however, perimeter may be one of the most concrete concepts we teach at primary level mathematics.
Research shows that human beings have a greater chance of remembering something if it is part of a meaningful experience, so before children in my class simply equated perimeter with rectangles, we stepped into the garden to make a memory.
What is perimeter?
Begin by introducing the concept of perimeter with a maths in real life example. I took my children outside, sat everybody down and walked around the edge of a marked area (being mindful to clearly model ending in the same position as I began).
I asked for a volunteer to copy what they had observed. Then another. I asked: what did you do to copy me exactly? Here the children dictated the rules on what success looked like based upon what has been modelled. Attention, engagement and a critical eye equalled success.
Taskmaster activities KS2
Then, ask the children to go into the garden or playground and find two leaves. In real Taskmaster style, I gave children five minutes to find and retrieve the two leaves that they agreed were the most visibly different.
The children worked in their learning pairs for this activity, to promote talk and collaboration. Circulate the group and listen for those pupils who are already conjecturing about shape, width, length, sides or edges!
Predict perimeters
Once the leaves are collected, the real excitement can then begin. Inform children that you want to measure the outside of the leaves using string.
Ask pupils to predict which of their leaves they think will use the most string and why. Is it because of the number of sides? Is it due to the length or width?
For my Year 3 children, this was a great opportunity to practise the skill of sifting the wheat from the chaff. Which qualities of the leaf were relevant and which needed to be left on the playground?
Start measuring
Now it is time to measure! Begin by modelling to the children how to use the string to measure the perimeter of a leaf.
Go back to the success criteria identified at the beginning of the lesson (e.g. measuring around the outside edge, starting and finishing at the same point and not over or under-measuring). Again, use learning partners to support your children to be successful in their accuracy.
Mark the lengths on the string and encourage pupils to use a ruler or metre stick to measure the string – this is a great chance to practise using a ruler!
Feedback
Finally, take the time to reflect and discuss what has been discovered in the session. Are children surprised by the perimeter of a seemingly ‘small’ leaf?
As children progress through perimeter, and take on area too, the appearance of a shape often throws up misconceptions.
Take this time to apply their initial thinking and give children different regular and irregular polygons and ask them to predict which would have the larger perimeter.
Lydia Davison is a KS2 teacher, with responsibility for Maths and Cognitive Science at a 3-11 primary school in Leicestershire. Follow her on Twitter at @davisonmiss.
How to recap the four basic operations by teaching perimeter

Revisit the four basic operations with these perimeter lesson ideas from much-missed Beth Smith at White Rose Maths…
How can you teach place value and the four operations in autumn term, without the need to revisit later?
We panic that children will forget the basics as we cover the many other areas of the curriculum. We refer back to the National Strategies, which saw children recovering content every term with a cyclical approach.
However, my advice is not to panic. As well as revisiting key skills daily, be reassured that you don’t just leave place value and the four operations behind. You in fact use them in other areas and can apply understanding across the curriculum. The national curriculum states:
The programmes of study are, by necessity, organised into apparently distinct domains, but pupils should make rich connections across mathematical ideas to develop fluency, mathematical reasoning and competence in solving increasingly sophisticated problems.
Rich connections
With this in mind, here I focus on perimeter and look at how we can encourage KS2 children to develop rich connections and deepen their understanding.
Perimeter lends itself perfectly to applying the four operations. Take this question from the White Rose Maths Y4 module: Work out the perimeter of the rectangles.
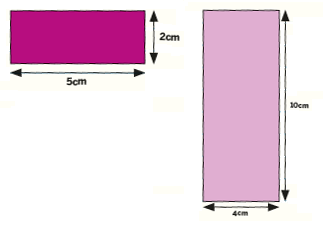
Here, children are working with numbers they can calculate mentally. Working out simple perimeters gives the perfect opportunity to share different methods and reasons about why each method works.
For example, one method is adding the length and width together and doubling this. Another is to label all the sides of the rectangle (opposite sides are equal), then add all four sides together.
Ask the children which method is more effective. Would you change your method if the length and width were 7.82m and 4.38m? Why? Delving deeper into children’s methods ensures they are confident in why the method works and why it is the most efficient.
Methods and reasons
This question can also be used to look at the difference between the perimeters of the rectangles. Children can reason about why the green rectangle is double the perimeter of the yellow rectangle.
They may then explore if, when you double both side lengths, the perimeter doubles as well. This shows how a fluency question can be extended through deeper questioning to encourage children to start to reason about a topic.
Using multiplication and their knowledge of shape, children can calculate perimeter where only one side length is given.
Within Y4, they can focus on squares. However, as they move into Y5 and learn about regular polygons, this can be consolidated by using times table knowledge to calculate the perimeter of regular pentagons, hexagons and octagons, for example.
Shape and division
Building on their knowledge of inverse, here is an example of a question that draws on understanding of shape and division: The perimeter of a square is 16cm. How long is each side?
Children need to understand that all the sides are equal in order to realise they need to divide by four. In order to use short division, children could be given the same question but with a larger perimeter, perhaps 532mm.
Ask children to convert from millimetres to centimetres to bring the skill of dividing by 10 into the mix. Drawing these skills together, here is a question taken from the White Rose Problem of the Day collection: Here is a rectangle.
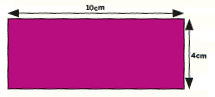
A new shape is made up of three of these rectangles.
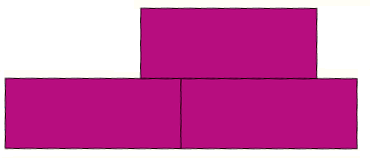
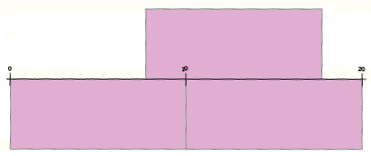
What is the perimeter of the new shape?
Finding the perimeter of one rectangle is simple. However, children need to reason in order to calculate the lengths of the sides where the rectangles join together.
Consider using a number line to support this understanding, once again drawing other aspects of the curriculum together.
Other rectilinear shapes
Moving on to other rectilinear shapes, I was inspired when working with a Y4 team at Lily Lane Primary in Manchester.
We were discussing ways to help children understand why we can use our understanding of the perimeter of rectangles to support calculating the perimeter of other rectilinear shapes.
We planned an investigation where the children had to find the perimeter of Numicon shapes. They could start by using each individual square as a unit, eg the number 10 Numicon has a length of five and width of two, therefore the perimeter is 14 units.
Developing this further, if you measure the length of one of the squares, the children can use multiplication to calculate the perimeter in centimetres as well as converting to millimetres.
Comparing the perimeter of different Numicon shapes will help children to uncover that some of the Numicon pieces have the same perimeter as each other even though they are different shapes. This can then lead children to look at a variety of rectilinear shapes.
Open-ended questions
Open-ended questions regarding perimeter give teachers the perfect chance to draw on knowledge from many areas of the curriculum. Take this question from the Y5 perimeter module of White Rose Maths:
How many rectangles can you draw where the length and width have a difference of five centimetres? What is the perimeter of each rectangle?
To begin with, children may focus on whole numbers (eg 12 centimetres and seven centimetres). However, teacher questioning can then encourage children to think more deeply about the length and width they can use:
- Will the length and width ever both be odd numbers? Will the length and width ever both be even numbers? Can you explain why?
- If the width of the rectangle is 34.5 centimetres, what will the length be? Can you write the length and width as a fraction?
- If the length of the rectangle is 21 centimetres, what will the width be? Can you write the perimeter as a decimal?
- The perimeter of the rectangle is 35 centimetres. The length and width have a difference of five centimetres. What is the length and width of the rectangle? Explain how you found your answer. Can you use a bar model to show your working?
Single question
These extension prompts show how teachers can take a single question for their whole class and use questioning to extend children’s thinking.
Children will draw on other areas of the curriculum and recap key skills in a different context, strengthening their understanding.
In conclusion, perimeter can be used to draw together number from across the curriculum. However, the same can be done with many other areas.
It is important that teachers plan for these links so that children can use, apply and deepen skills in all areas of the maths curriculum.
Beth Smith was senior primary maths specialist for whiterosemaths.com.











