Primary school maths – use visual representations to make adding and subtracting more interesting

From surprising patterns to solving puzzles, get a bit more playful with calculations

We love doing mathematics when it enables us to be creative, when it uncovers surprising patterns and when it gives us the opportunity to find novel solutions. At its best, maths gives us a chance to think divergently and approach problems in different ways, and to be mentally playful.
When I describe maths in this way, you probably think of your favourite problem-solving task, and rightly so. I love the buzz of the classroom while children grapple with an exciting logic puzzle or an open-ended Nrich task.
But what if we could take some of the traditionally more routine aspects of maths and open them up to more wide-ranging ways of thinking too? Even in addition and subtraction!
Adding and subtracting
A big emphasis is placed – quite correctly – on developing children’s mental fluency in addition and subtraction within 20. So, for example, we hope that learners develop a range of strategies for deriving the answer to 7+5, supported by practical experiences and visual representations, like 10-frames.
We encourage pupils to make a 10, seeing the 5 partitioned into 3 and 2, and want them to notice that 7+5 is 2 more than 5+5, by partitioning the 7 into 5 and 2.
We may also draw out that 7+5=6+6 by moving one counter from the left 10-frame onto the right 10-frame. Now we can use our doubles facts, too, in order to find the answer.
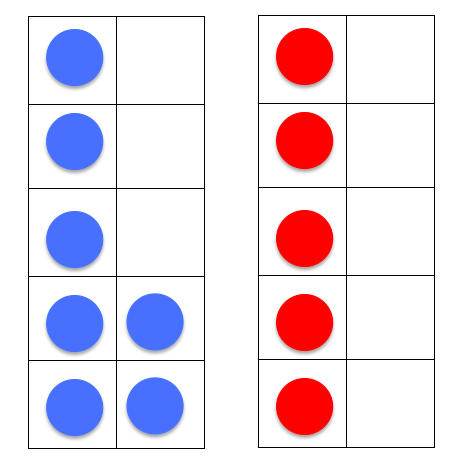
Similarly, let’s consider the different strategies that children can use for calculating 13 – 8. I like to show children 13 on two 10-frames. Then I ask them where they visualise the 8 being subtracted from: the left 10-frame, the right 10-frame or both 10-frames?
Subtracting from the left 10-frame encourages a ‘counting-on’ thought process. When subtracting from both 10-frames, pupils are encouraged to see the parts of 3 and 5 being subtracted. Again, we can promote different calculation strategies here.
Mental maths methods
By developing a range of efficient mental methods for addition and subtraction within 20, children will become genuinely fluent and we can encourage them to start choosing the best method for any given calculation.
How, then, can this ethos be continued when pupils progress to adding and subtracting two- and three-digit numbers? If we revert to working predominantly in the abstract, children often end up using written methods to perform every calculation.
But in coming back to the visual representations, and by celebrating the different methods that learners can use, we continue to develop these flexible, diverse calculation strategies.
For example, when representing 27+26 as quantities in 10-frames, maybe children will suggest moving 3 counters to change the calculation into 30+23.
Perhaps they will suggest adding the 10s then adding the 1s. Or maybe they will also recognise that they could calculate double 25 plus 3.
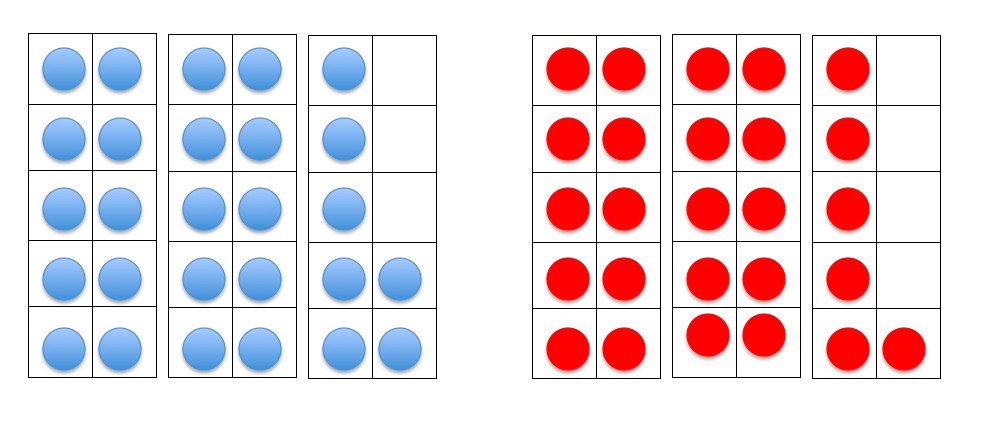
Again, all these strategies can be modelled and celebrated. From this foundation, as children progress into performing a calculation like 297+154, they can come to recognise that the answer will be equivalent to 300+151.
Think big
These big ideas can be explored further even as pupils practise calculation methods. Consider, for example, this sequence of three questions:
573+245=
543+275=
537+281=
Children are likely to calculate the answers using a column method. And if they answer the questions correctly, what will they discover? That all the answers are the same!
Why? Well, the only difference between question one and question two is the position of the 10s values within the addends. This doesn’t affect the sum. And we can explain the link between question two and question three by explaining that 537 is 6 less than 543, and 281 is 6 more than 275; therefore, the answer is the same!
By putting the questions in this sequence, as well as practising their calculation skills, children are exposed to these big mathematical principles and have more opportunities for reasoning mathematically.
The key idea that I focus on in subtraction is ‘constant difference’. So, for example, we might start by giving children sequences of questions like this…
9-6=
8-5=
7-4=
…and then using a visual representation to show that when the minuend (the number from which we’re subtracting) and subtrahend (the number to be subtracted) increase or decrease by the same amount, the difference between the two numbers remains the same.
This is a pattern that I will keep coming back to throughout lessons, and this idea can then be explored in a larger number range. For example, we can recognise that 41–18, 43–20 and 39–16 all have the same answer.
However, we might also see that some of the calculations are easier to perform than others!
Now, let’s consider another short sequence of questions that can draw children’s attention to these big ideas, as well as giving them the opportunity to practise their written calculation methods. Have a go at answering these three questions:
558–233=
564–239=
584–219=
The first question can be calculated relatively easily using a column method, as regrouping is not needed to find the answer. Question two does require regrouping, but having found the answer to question one, children might notice that the answer to this is actually the same.
Why? Because the minuend and the subtrahend have increased by the same amount. And for question three, pupils may expect the answer to be the same as question two if they recognise that the minuend and the subtrahend both change by 20. But, of course, the minuend increases by 20, whereas the subtrahend decreases by 20.
This means that the answer to question three will be 40 more than the answer to question two. Children might even notice this before they carry out the calculation, but they normally complete a written calculation to check their theory. This is such a rich opportunity for reasoning and pattern spotting.
Of course, for children to have sustained success they need these methods and approaches to be promoted consistently, year upon year, using visual representations and reasoning techniques.
It’s not a fast road, but it promotes rich and diverse thinking. By focusing on these big ideas and relationships, children are given the tools to approach mathematics with curiosity and flexibility, and we tap into a deeper expression of what it is to be a true mathematician. For me, these ideas have brought previously dry aspects of the maths curriculum to life!
Gareth Metcalfe is the director of I See Maths and author of the I See Reasoning and I See Problem-Solving eBooks. Follow him on Twitter @gareth_metcalfe












