Primary maths – Why are so many maths lessons based on recalling abstract, unrelated algorithms?

If we value children’s creativity, why are so many maths lessons based on recalling abstract, unrelated algorithms, asks John Bee…

- by John Bee

“I like maths because it has a right or wrong answer.” This sentence can be heard in classrooms across the UK, but is maths providing us with a false sense of security? Is there more at play?
We’ve all looked at fractions with terror in our eyes, wondering whether the ‘top number’ is the numerator or denominator.
Do we need to keep or change the denominators so they are equivalent? What about keeping, flipping and changing the digits? Is ¼ > ⅕? Multiplying fractions is easy: just multiply the ‘top number’ by the ‘bottom number’.
This kind of approach relies heavily on following and remembering rules and procedures. Debate, reasoning and even thinking become limited. As a profession we celebrate the creative and imaginative capacity of children.
Why, then, do some maths classes become elaborate lessons in remembering the particular rules of abstract, unrelated algorithms?
Of course, we should not underplay the importance of algorithms and mathematical fluency, but this should be an end goal of teaching once children have mastered concepts, not the dominant pedagogy or approach.
Most teachers know how and why algorithms work; children less so. It’s our job as teachers to expose mathematical structures to make abstract processes concrete and clear.
Under this lens, it is not difficult to see why around a quarter of children do not reach the expected standard for mathematics at Y6.
In a curriculum which places emphasis on procedural, unrelated facts, children may miss the connections within maths, such as how learning to count in twos, threes, fives and tens in KS1 links to reading and interpreting scales on graphs in KS2, or how learning about factors and multiples helps when solving problems linked to fractions.
It’s essential that children make links if they are to think like mathematicians.
Some teachers already use reasoning and allow children space to think and justify, but do we already have set parameters for success? Are we only looking for reasoning which ultimately arrives at a given answer? If so, how do we move away from a right/wrong culture in maths?
Putting debate, discussion and reasoning at the centre of lessons can transform teaching and learning and, ultimately, the culture of mathematics.
Here are five principles to adhere to.
1 | Start with a genuine question
A few years ago, I used to watch the Saturday night TV show Take Me Out, in which an array of girls looking to go on a date would switch off their light if they were not interested in the man who emerged from the ‘love lift’.
Making children write down a dry learning objective such as “To add fractions” instantly turns the lights off behind their eyes.
Consider the below examples:
Example 1
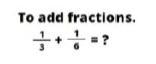
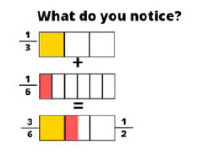
Example 2
The first example requires memory of the algorithm and rules.
The second, however, provides the answer but elicits children to explain using equivalences, models and images to understand how and why the algorithm works.
You don’t even need to mention the word ‘fraction’ initially.
2 | Ditch calculation lists
When presented with a list of unrelated calculations, children rely on a process or memory. However, as soon as they arrive at an answer, the thinking stops. An alternative is to offer different models or images that pupils need to match or write calculations for.
For example, show the numbers 151 and 515 and ask what is the same and what is different. This can lead to powerful transformative discussions.
Similarly, showing models of fractions and asking what pupils notice encourages debate, justification and reasoning.
3 | Avoid ‘yes’ and ‘no’
You may be the teacher, but you’re not the answer sheet. As soon as you say ‘yes’ or ‘no’, you limit pupils’ thinking and reasoning. Instead, ask why or how a concept works. This is an effective way to strengthen and deepen children’s understanding.
4 | Explore children’s ideas
To be told ‘no’ by a teacher is disempowering and disengaging. To have your answer proven wrong by peers is a learning experience. Encourage exploration, drawing, creating and designing in your maths classroom to bring debate alive.
5 | Get creative
Use practical equipment, models and images to spark discussion, debate and reasoning. Double-sided counters are great for revealing mathematical structures.
For example, displaying four counters with two red sides up and two yellow sides up shows that 2/4 is equivalent to ½.
John Bee is head of KS2 and maths leader at a primary school. He is the author of Maths Mastery Reasoning: Photocopiable Resources KS1 and KS2 (Bloomsbury Education). Find him at mrbeeteach.com and follow him on Twitter at @mrbeeteach











