Once Upon A Times Table – Turn Maths Into Stories To Help Children Learn

In this year’s SATs, nearly 60% of children failed to answer a question on fractions. Had they turned it into a story, it would have made a lot more sense.

- by Mike Askew

Sadly, Jerome Bruner, one of the great thinkers of educational philosophy and psychology, died recently. He is probably best known for highlighting the importance of the concrete, iconic and the symbolic (now commonly referred to as the concrete pictorial and abstract).
Perhaps less well remembered, though, is the importance Bruner placed on narrative in teaching, because, he claimed, “People and their actions dominate the child’s interest and attention.”
I would agree. Much as I love mathematics, I think most people would rather watch EastEnders than play with a mathematical challenge.
With this in mind, it seems right to question whether we give narrative enough attention in mathematics teaching. Can we improve children’s understanding by tapping into their interest in people and their actions?
Narratives in mathematics often begin and end with word problems – little stories that act as window dressing. But the issue with wrapping calculations in words, as shown in lots of research, is that when children encounter a problem within a narrative, they often hone in on the numbers without really paying attention to the context.
A classic example of this is an assessment question that asked upper primary pupils what the temperature of 2 litres of water would be if 1 litre of water at 25℃ were mixed with 1 litre of water at 75℃. The majority answered 100℃, ignoring the fact that this would mean the water was then boiling.
Narrative is important in two ways. Firstly, we can better understand realistic problems (or narratives) by drawing out the mathematics. But, as regular readers will know, I’ve written about this before, so I want to look at the second use: how starting from a ‘bald’ mathematics calculation and thinking about what story could describe it can help deepen the understanding of ‘pure’ maths.
How stories make sense of sums
Think about this calculation from this year’s key stage 2 arithmetic paper:
1 1/4 – 1/3
I recently asked some learners to think of a story that would result in having to do this calculation? Broadly, although the contexts differed (cakes or drinks, say, instead of pizzas) two different types of narrative emerged. The first was broadly along the lines of the following:
I’ve got one and a quarter pizzas in the fridge and I will be sharing this with my two friends. But I’m hungry so I eat a third of the pizzas. How much pizza is left in the fridge?
The second version that emerged was:
I’ve got one and a quarter pizzas in the fridge and I eat a third of a pizza. How much pizza is left in the fridge?
You might like to consider which of these two interpretations you would go with.
As a teacher, getting two different answers like this poses a challenge: do you ‘correct’ the learners you think have given the wrong answer? Or does the disagreement itself become a resource for learning? For me, it’s the latter – it’s a great opportunity to ask, “What is the same and what is different?”
On the surface the problems look very similar. The question is the same in each case: one third of something is removed. But a crucial difference is the distinction between “I eat a third of the pizzas” and “I eat a third of a pizza”. The underlying mathematics that each of these provokes is very different. In the first problem I have to subtract one third of the total quantity of pizza. In the second problem I subtract one third of a single pizza.
A quick sketch of each situation makes the difference clear.
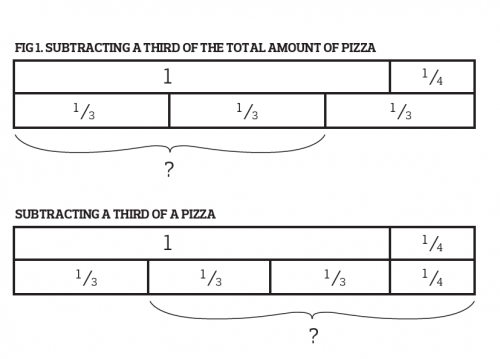
Looking for sensible answers
The question remains as to which interpretation is correct? And do I just tell my learners the answer? I would suggest not, but the teaching that follows depends on slightly altering the question from “Which is correct?” to “Which makes the most sense?” This shift, although subtle, makes a big difference.
Knowing which is correct relies on an external authority telling you the answer, since it’s not possible to reach this conclusion by just looking at the examples. This reinforces the view that mathematics is a set of rules determined by someone else – rules that you, the learner, just have to accept.
But asking asking “Which makes the most sense?” invites learners to think further, to reason, or, in other words, to act as mathematicians. Variation can help with this, by which I mean thinking about what to keep constant and what to change in creating further examples.
So, we might decide to keep the part of the story about the fridge being raided, but change the amount eaten to 1/2 and vary the starting amount (to four pizzas, in the first instance). This makes our new bald calculation:
4 – 1/2
Everyone was agreed that the answer to this was 3 1/2 (‘four subtract one half’; not ‘half of four’). So the narrative version of the problem is:
I have four pizzas in the fridge and come home and to eat 1/2 a pizza. How much pizza is left in the fridge?
And what about if we change the bald calculation to this:
2 1/4 – 1/2
Yep – two and a quarter pizzas in the fridge and I eat 1/2 of a whole pizza.
So, returning to 1 1/4 – 1/3, the sensible interpretation is that it is 1/3 of a single pizza eaten, not a third of the whole amount.
From SATs to deep maths
In the actual test, only 41% of learners got that question correct (and 81 per cent attempted it), so obviously it was not easy. So how might we help more children get it right?
Given the question was on the arithmetic paper – not reasoning – it’s tempting to give learners lots more practice at this type of calculation. But I would argue that, even if that lead to more learners getting the correct answer, an opportunity for integrating problem solving and reasoning will have been missed. Here is a chance to explore a big idea in mathematics – that of absolute or relative change.
Relatively speaking
The writer Susan Lamon has a lovely thought experiment that illustrates the difference between the absolute and relative.
Imagine five people. Now think about them in these different situations:
• Five people in an eight-person lift • Five people in Wembley Stadium • Five people in a Mini
Do you get a sense that some of these situations are more claustrophobic than others? The absolute quantity – five people – is constant in each case, but the amount of space is relative.
One of Lamon’s suggestions for helping children get a sense of this difference is to start with a simple narrative, for example:
Mike has built a tower with six cubes and Russell one with four cubes.
Then ask a series of questions and think about whether they involve absolute or relative thinking. E.g.
• Who has more cubes, Mike or Russell?
• How many times would you need to stack up Russell’s cubes to get a tower as tall as Mike’s?
• What part of a dozen cubes does Russell have?
• How many fewer cubes does Russell have than Mike?
• Russell and Mike have three red cubes. What percentage of each boy’s tower is red?
• How many more cubes does Mike have than Russell?
• How many cubes do Mike and Russell have altogether?
• The boys put their cubes together and share them with three other friends. What part of the collection of cubes will each child get?
Not just arithmetic
Going back to the test question, what I had expected to be a quick look at a ‘simple’ calculation from the arithmetic paper provided a rich (if unexpected) opportunity for something more. We were not only able to work on how the calculation might be solved, but also to develop and deepen learners’ understanding of what gives rise to subtraction fractions. Over and above this, it opened up a rich seam of work on a key distinction in mathematics – additive reasoning (absolute change) and multiplicative reasoning (relative change). All from one, on the surface, rather dull calculation.
TEACHING CHILDREN TO UNDERSTAND FRACTIONS
One of the myths about fractions is that they are something we can ‘recognise’. The trouble (and strength) of fractions is that they can represent so many different things and be represented in so many different ways. Children can’t learn every permutation; instead, we have to help them reason about fractions – about what they mean and where they come from (even if our goal is only using them to carry out calculations).
Susan Lamon’s book, Teaching Fractions and Ratios for Understanding, is a treasure trove of ideas for helping learners to develop a deep understanding of fractions, and I highly recommend it.
Mike Askew is professor of mathematics education at the University of Witswatersrand, Johannesburg as well as freelance, teacher, researcher and writer about primary mathematics (mikeaskew.net). Take a look at our Year 2 maths worksheets.











