KS3 Maths Lesson Plan: Exploring Number Patterns And Where They Appear In The Real World

The way in which the pages are numbered in a newspaper gives opportunities for students to explore number patterns and structure

- by Colin Foster

Patterns in numbers arise in many different circumstances in the world around us. Making sense of these with mathematics allows students to use their mathematical knowledge and develop their appreciation of mathematical structure.
Sometimes students are asked to complete arbitrary patterns such as 1, 2, 4, 8, 16, … However, there are always multiple possible answers to these, depending on the “secret” rule that the person devising the sequence has used.
This means that there is often as much psychology as mathematics in questions like this – the student has to guess what kind of pattern the person who invented the sequence is most likely to have used.
In this lesson, the number sequences arise from real situations in which the rules are known, but working out how the sequences will develop is not straightforward.
Starter activity
Seat students in groups of 4 or 5 around tables. Before the lesson, take a pile of old newspapers and choose and remove one double sheet from each newspaper.
(Make sure that the sheet has the four page numbers printed on it, and obviously ensure that there is nothing inappropriate on the sheet that you select.) The newspapers could be a variety of different ones or just different days’ issues of the same one – it doesn’t matter. Bring to the lesson the sheets that you have removed.
Q. I am going to place an object on each table and I would like you to write down everything you can work out about what it is and where it has come from. Place one sheet on each table. Give students a few minutes to make a list of what they can deduce.
Q. What were you able to work out? The might be able to identify the name of the newspaper that their sheet came from, the date that issue was published and which section of the newspaper the sheet is from. They might also be able to draw some conclusions from the content.
Q. What mathematical questions can you ask about your sheet? Students may find this difficult and think that there is one particular question that you want them to think of (guess what is in your mind). You could emphasise that there isn’t one right answer and you would just like them to think of as many different things as they can that link the sheet that they have been given to mathematics.
For example, students might ask how much it costs to print a newspaper, how fast one sheet can be printed, how much profit can be made from selling newspapers, how much ink it takes, how many newspapers are sold each day in the UK or the world, how high a stack those newspapers would make if they were all piled on top of one another, what proportion of readers read the paper online, and many more things. Being able to think of questions to ask is an essential skill if students are to be able to use mathematics to enquire into the world around them.
Main activity
Someone may have already suggested this question – if not, you can suggest it now.
Q. Can you work out how many pages there are in the newspaper that your sheet has come from? Give students some time to discuss this in pairs and work out what they are going to do. They will realise that the four page numbers on the double page sheet that they have been given might enable them to do this.
Some pupils might want to construct a replica of the paper and number all the pages. It might be better to discourage this by not providing enough scrap paper for that to be possible. It would probably be more useful for pupils to try to reason it out. However, you could invite pairs to construct a 16-page (say) “newspaper”, so as to discover how the page numbers on the same double-page are related.
This might then help them to work out what is going on with a larger newspaper with more than 16 pages.
With 16 pages, we have 4 sheets of paper (page numbers in brackets are those on the reverse side of the sheet):
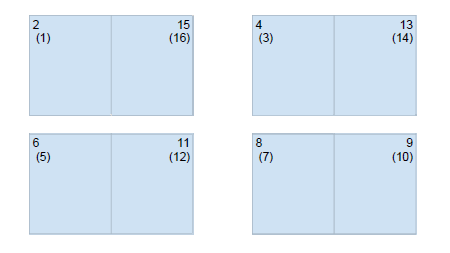
This should be enough of a start to help students to begin to see some patterns and make some conjectures about how the page numbers work more generally.
When students are satisfied with their answer regarding the total number of pages in the newspaper that their sheet came from, they could be invited to make up (and answer) questions for each other, such as: “For a 64-page newspaper, which other three page numbers come on the sheet that has page 42 on it?”
Discussion
You could conclude the lesson with a plenary idea in which the students talk about their solutions and how they got them.
Q. Did you manage to work out the number of pages in the newspaper that your sheet came from? How confident are you that your answer is right? Why? How did you do it? What did you find out about how page numbers work in newspapers? What problems did you make up?
If you still have the original newspapers, students might like to see confirmation of their calculations by looking at the page number on the back page.
Students will have noticed that the right-hand pages have odd numbers and the left-hand pages have even numbers. They will also have noticed that back-to-back page numbers always differ by 1, so one is always odd and the other even.
They may also have noticed that as you move from one sheet to the next one in towards the middle of the newspaper, the first two page numbers on the sheet increase by 2 and the last two page numbers on the sheet decrease by 2.
Crucially, this means that the total of the four page numbers on a sheet is constant from one sheet to the next. This means that we have found an invariance – something that doesn’t change – which is often extremely useful in mathematics.
If our newspaper has n pages, then the first (outer) sheet will contain pages 1, 2, n – 1 and n, which sums to 2n + 2. This will therefore be the sum of the page numbers on any sheet in the paper.
For example, the next sheet in will have page numbers 3, 4, n – 3 and n – 2, which also sums to 2n + 2. So if S is the sum of the page numbers on our sheet then is the total number of pages in the paper.
So finding the total number of pages given just one sheet is not too difficult. However, creating valid problems like this is a bit harder. Students cannot just pick any four numbers as the four page numbers of a sheet, as they must be two consecutive pairs, both beginning with an odd number.
Algebraically, a newspaper with n pages will have, on the rth sheet from the front, pages numbered 2r – 1, 2r, n – 2r + 1 and n – 2r +2. We can see that the total of these comes to 2n + 2, since the rs cancel out.
Additional resources
A nice related newspaper problem is available at nrich.maths.org/44.
Stretch them further
Students could be invited to think about how the pages should be arranged on a large sheet before being folded and cut up to make the newspaper. Some will need to be placed upside down to make it work. Students could also investigate what the “Print Booklet” option does in design software.
KEY RESOURCE
Algebra Project – Introduction to Algebra and Solving Equations If you are looking for a way to improve your learners’ algebraic understanding and support progression in algebraic reasoning this is a brilliant resource from the Association of Teachers of Mathematics.
There are 200 pages of carefully considered starting points, resources, approaches and guidance that are designed to (a) be accessible to the learners and (b) support the teachers in improving the learners’ algebraic understanding while sorting out misconceptions. One mathematics teacher who used the Algebra Project wrote “ I thoroughly recommend it for mathematics teachers in secondary schools” atm.org.uk/shop/ADD001pk
Colin Foster is an Assistant Professor in mathematics education in the School of Education at the University of Nottingham. He has written many books and articles for mathematics teachers (see foster77.co.uk).











