KS4 Maths Lesson Plan – Using Number Patterns To Understand Integers
Calculations involving multiplication of whole numbers don’t have to be boring if the answers contain surprising patterns

- by Colin Foster

Understanding when one integer will divide exactly into another helps students to ‘make friends’ with the integers and feel more secure when carrying out calculations.
It also often enables short-cuts, such as noticing things like:
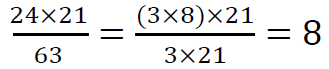
Even when students are using calculators, this sort of familiarity with factors enables students to estimate the sizes of answers (and such things as whether an integer should be obtained or not).
All of this provides valuable checks on the work that they are doing and can be more intellectually stimulating than merely following standard algorithms to get an answer. It also enables students to be sure, for example, that a number like 111,111,111,111,111 is divisible by 3, even though their calculator would probably only be able to give an approximate answer to this:
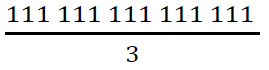
In this lesson, students have the opportunity to experiment with producing ‘nice’ answers like 123,456 from multiplying integers.
Starter activity
You could allow students to use a calculator for this or alternatively use it as an opportunity to reinforce written methods of calculation.
Q. Think of a 3-digit number, like 738, for example, where all three digits are different. Write it down. Now I want you to multiply your number by 7. Now multiply your answer by 11. And finally multiply your answer by 13.
Just wait for a reaction – if none comes, you could ask: Q. Do you notice anything?
If students do it correctly, they will obtain a six-digit number consisting of their original number repeated twice, so starting with 738 they would obtain 738,738. Unless they have seen this trick before, they will be surprised, and perhaps intrigued.
Q. Why did that happen? Will it always work?
Give students a bit of time in pairs to talk about it. They may realise that multiplying by 7, then 11 and then 13 (in any order) is equivalent to multiplying once by 7 × 11 × 13, which happens to be equal to 1,001.
They may need to think about a number like 738,738 as 738,000 + 738 (a thousand lots of 738 plus one more lot of 738). This is a good opportunity to think about place value. Students might talk informally about putting 738 “in the thousands column” and 738 “in the units column”.
Students may be surprised that 7 × 11 × 13 = 1,001 – all those awkward digits leading to the neat number 1,001. They may also wonder how you could begin with the idea of 1001 and then discover this factorisation if you didn’t already know it. (It is also neat that 1001 is the product of three consecutive primes.)
Q. Can you make up a trick like this?
This is hard, depending on how students interpret “like this”. They might think that if they could find factors of 1,000,001 (= 101 × 9,901) then they could do a similar trick starting with a six-digit number.
This is fine mathematically, although the final answer will appear in standard form on a calculator, which is likely to be confusing. It would be simpler to use a four-digit number multiplied by 10,001 (= 73 × 137) to give an eight-digit answer, or a five-digit number multiplied by 100,001 (= 11 × 9,091) to give a 10-digit answer. However, these factorisations are hard to find by hand!
Another possibility would be to stick with a three-digit number but multiply by 1,001,001 (= 3 × 333,667) to give three repetitions of the starting number (eg, 738 × 3 × 333,667 = 738,738,738). Or maybe just start with a single-digit number (eg, 6) and multiply by 111 (= 3 × 37) to obtain a repdigit (eg, 6 × 3 × 37 = 666).
Main activity
Q. I would like you to work out 15 × 823, please.
Students may think this is a very boring thing to ask them to do. If they approach it reluctantly, that is all right, as they will get a surprise when they do it! Again, depending on the class and your intentions with this lesson, you could either let them use calculators or not.
Students will be surprised when they find that the answer is 12,345. They might say, “Wow” or “Cool” or “How did you do that?”
Q. Can you make up one that does that?
‘One’ and ‘that’ is deliberately left vague here so that students can interpret for themselves what is special about this product and what they might wish to try to reproduce. If students have no idea what to do, you could suggest that they see if they can find two integers with a product of 123,456, or, if they want an easier start, 123.
Approaching this by trial and error is hard, although they might think of 1 × 123,456, which is a good start!
Give them some time to experiment. Students will need to use calculators to test their ideas, but should be discouraged from mindlessly trying number after number.
For example, they could look back at the answer 12,345 from above and note that it ends in a 5, so must be a multiple of 5. They might also find that its digits sum to 1 + 2 + 3 + 4 + 5 = 15, which is a multiple of 3, so 12,345 is also a multiple of 3.
Since it’s a multiple of 3 and 5 (and 3 and 5 are co-prime), it must be a multiple of 15. Then calculating 12345 ÷ 15 gives 823, so we obtain the product 15 × 823 as a way of making 12,345.
If students don’t know tests for divisibility such as these, you could stop everyone and ask: Q. Do you know any way to tell whether a number is a multiple of 5 without actually dividing it by 5?
You could collect on the board the tests that students know about, and add in ones (like 7) that probably no one knows.
For example,

In this table, ‘iff’ means ‘if and only if’ – in other words, if one of these tests fails then the number is not a multiple. Digital root means the digital sum (the sum of the digits) carried out repeatedly until just a single digit remains. Note that 0 is a multiple of every number, because, for example, 0 × 5 = 0, so 0 is a multiple of 5.
This should be enough of a start to help pupils to find some pairs of numbers that multiply to make ‘neat’ answers.
Discussion
You could conclude the lesson with a plenary in which the students share the products that they found and explain how they got them.
Q. What did you come up with? How did you do it? Which ones were difficult? Why? Did you find any of them easy to do? Why?
Students may have discovered examples such as 12 = 3 × 4 (nice because 1, 2, 3, 4 are consecutive), 123 = 3 × 41, 1,234 = 2 × 617, 12,345 = 3 × 4,115 or 5 × 2,469.
If they have access to an online factorising software (see ‘additional resources’ below), or their calculator will do it, then they may have found more complicated ones, such as 123,456 = 192 × 643, 1,234,567 = 127 × 9,721 and 12,345,678 = 846 × 14,593. There are many other possibilities, of course, such as patterns like:
234 = 13 × 18 2,345 = 35 × 67 23,456 = 32 × 733 234,567 = 389 × 603
1,111 = 11 × 101 11,111 = 41 × 271 111,111 = 231 × 481
64 × 15,625 = 1 000 000
Additional resources
There is a free online prime factorisation calculator at mathsisfun.com/numbers/prime-factorization-tool.html
Stretch them further
There is an article with more detail about divisibility tests at nrich.maths.org/1308.
Colin Foster is an assistant professor in mathematics education in the School of Education at the University of Nottingham. He has written many books and articles for mathematics teachers (see www.foster77.co.uk).










