KS3 Geometry – Exterior angles

Colin Foster looks at how teachers can prevent students from misinterpreting how the exterior and interior angles of polygons relate to each other

- by Colin Foster
This task is intended to bring to the surface possible confusions over exterior angles.
Look at the polygon below (download the accompanying task sheet for a printable version).
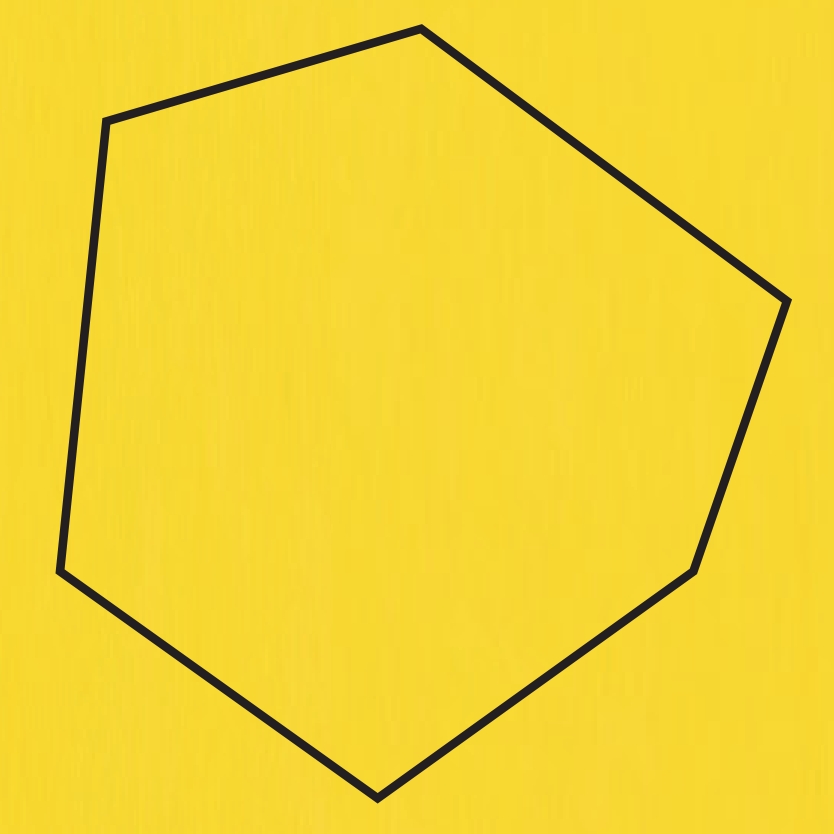
Clearly mark all the interior angles in red. Clearly mark all the exterior angles in blue.
Students will probably correctly mark the interior angles, as shown here.
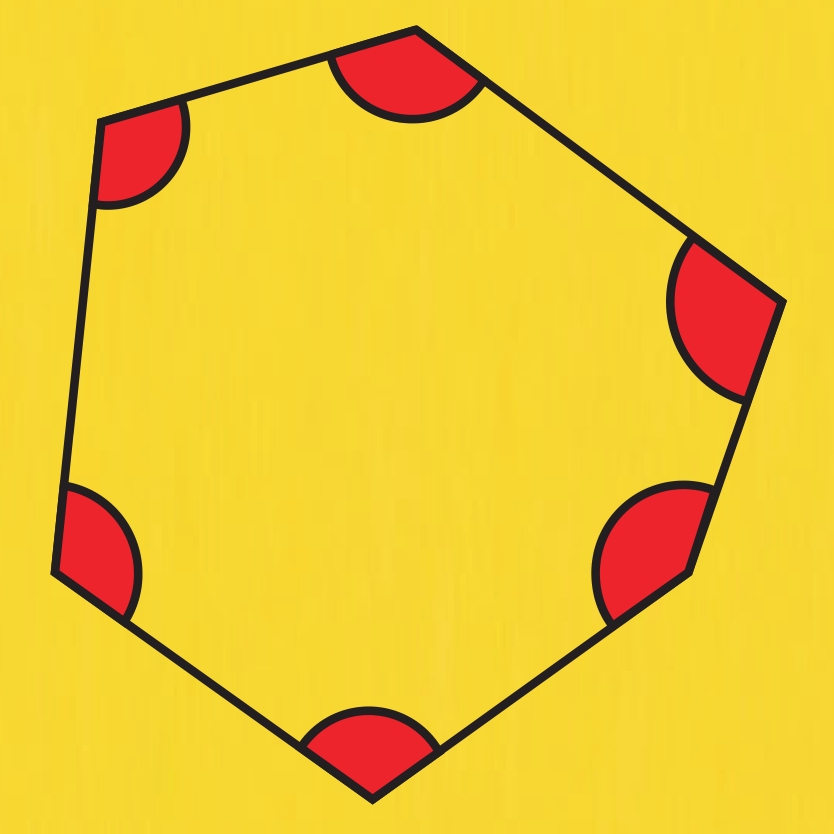
But some students are likely to incorrectly mark the exterior angles, like this…
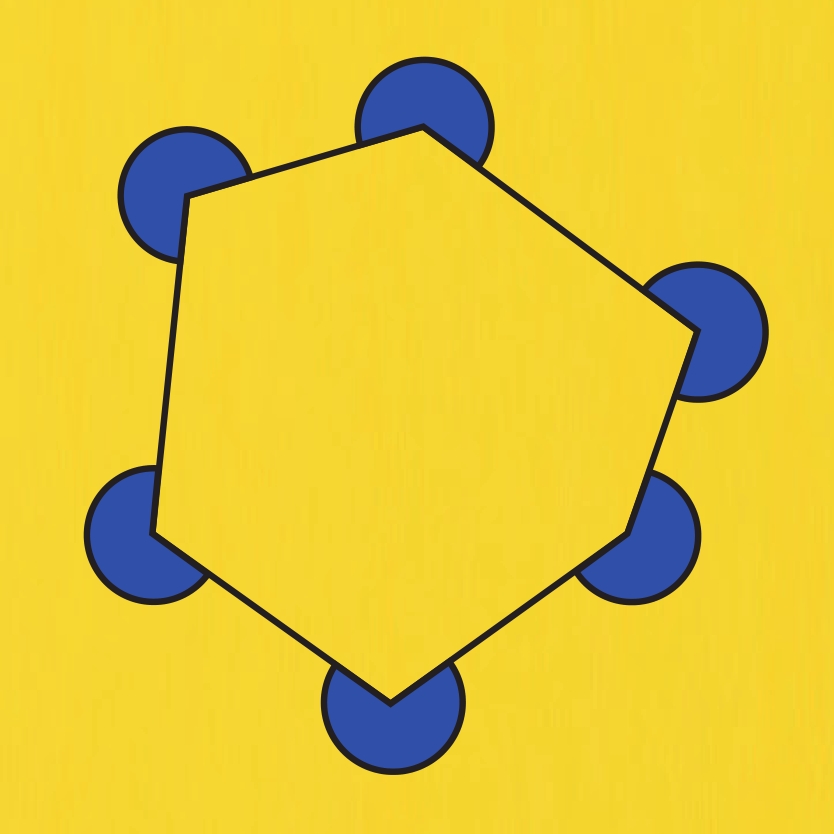
…rather than the correct answer, as illustrated below.
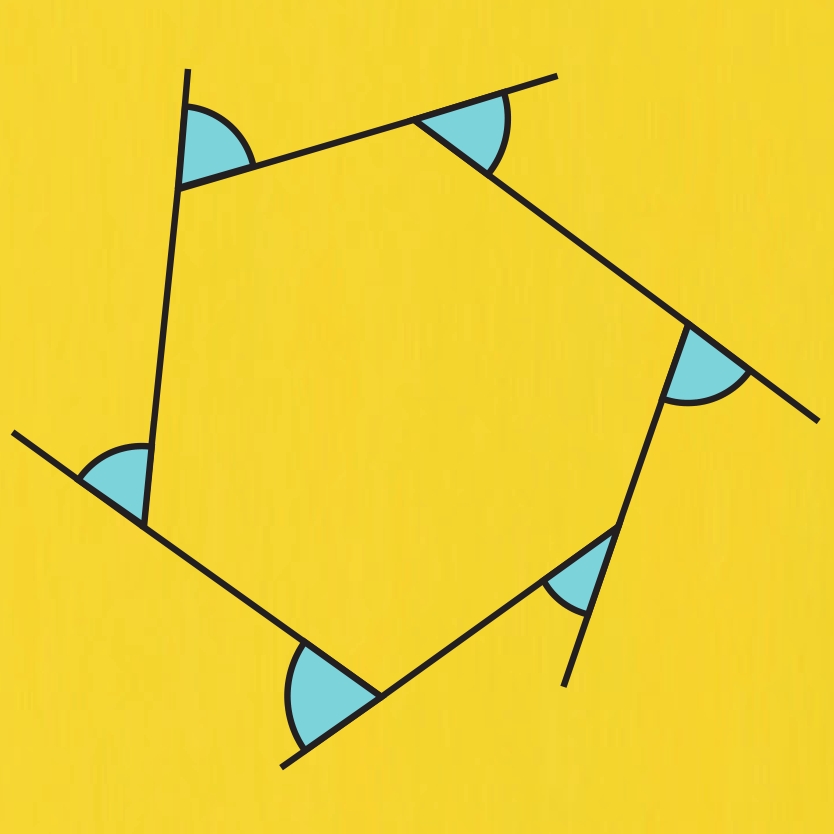
The solution
The light blue exterior angles are sometimes called ‘turn angles’, because they are the angles you would turn through if you were walking around the polygon.
How are the red, dark blue and light blue angles related to each other?
If students find this difficult, they might benefit from using protractors to check their ideas, or from making drawings of different polygon examples so they can check that their conjectures work.
Every light blue exterior angle is supplementary to the red interior angle at the same vertex:
red + light blue = 180˚ at each vertex
Every dark blue angle is the reflex angle of the red angle at the same vertex:
360˚ = red + dark blue at each vertex
Finally, every dark blue angle is a straight angle more than the light blue angle at the same vertex:
light blue + 180˚ = dark blue at each vertex
This third equation can also be found by adding together the first two equations (the red cancels out).
Checking for understanding
Conclude the lesson by asking students to see if they can write down general statements about these angles for an n-gon. (Here, with a hexagon, n = 6.)
The sum of the red angles = 180(n – 2)˚
The sum of the light blue angles = 360˚
The sum of the dark blue angles = (360 + 180n)˚
This means that the sum of all of the dark blue angles and all of the red angles must be (360 + 180n) + 180(n – 2) = 360n˚, which makes sense, because it corresponds to a full turn for each vertex.
Colin Foster (@colinfoster77) is a Reader in Mathematics Education at the Mathematics Education Centre at Loughborough University. He has written many books and articles for mathematics teachers. foster77.co.uk











