How to differentiate one maths problem for learners of all abilities

Having everyone tackle the same maths problem needn’t preclude the possibility of differentiation says Judy Hornigold…

Many schools are now adopting a whole class approach to teaching maths, where each lesson starts with all the children tackling the same problem. Consequently, one of the questions I’m most frequently asked is how it’s possible to differentiate effectively when everyone is doing the same thing.
In the past, teachers would became used to differentiating lessons by preparing three, four or sometimes even five entirely different lessons to meet the needs of pupils in their class at different levels, but there’s really no need to go to such lengths in planning.
If anything, doing so can often be counterproductive. The struggling children tend to remain struggling, while the more advanced children make greater progress.
The end result is that the gap between the two continues to widen, until it’s so great as to be almost impossible to close. Mathematics is a strange beast.
There are areas of it that some children find very challenging, and others they find very straightforward, so it’s impossible to predetermine a child’s level in every lesson – it really depends on the lesson content.
The approach used in Singapore is to teach the whole class, with the children sitting in mixed ability groups, and to differentiate the same problem by process, content or product. We can differentiate by our expectations and the questions we ask whilst everyone is engaged in tackling the same problem.
What are you asking?
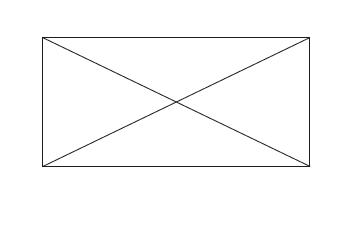
By way of an illustration, consider the following problem. In this mind workout, the children have been asked to discover if these triangles are all quarters of the rectangle. At first sight, it seems to some children (and some adults!) that the triangles aren’t the same. The triangles with the longer sides appear larger.
This problem can be differentiated in many ways. If the children are given paper and scissors, they can replicate the problem by cutting out the triangles and folding them in half to see that they are all, in fact, equal and therefore all quarters. This is harder to do without any paper and scissors to hand, as it requires more visualisation skills.
The problem can then be differentiated further by altering the way which the question is asked. If we now name the triangles ‘A’ and ‘B’ we can differentiate by asking ‘Do A and B have the same area?’
We might even ask, ‘What is the ratio of the areas of A and B?’
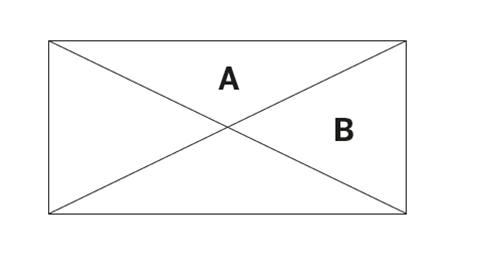
We have thus taken a question aimed at year 1 children and differentiated it to a much higher level that demands an understanding of area and ratio.
Scaling up
Another example of how we can differentiate with the same problem is shown above. Can you arrange five numbers so that the vertical total is the same as the horizontal total?
The expectation here is that the children will be able to find such an arrangement and quickly realise that if the top and bottom numbers add up to the same as the left and right numbers, then it doesn’t really matter what’s in the middle. We can change the middle number and the vertical and horizontal totals will still be equal.
The next level for the children may be to set a target. Can they find all the solutions that total 15? Can they do this using only odd numbers? Do they always need to have a mix of odd and even numbers?
For some children that will be enough of a challenge, but we can take this activity much further. Thinking like a mathematician, we may propose a hypothesis that the middle number is irrelevant, as it’s common to both calculations. But is this always the case? What if we have consecutive numbers?
Now we can ask the children to repeat the activity, but this time they can only use the numbers 1,2,3,4 and 5. They’ll soon discover that now it really does matter what’s in the middle. For this set of numbers, there are only three numbers that can be the middle number.
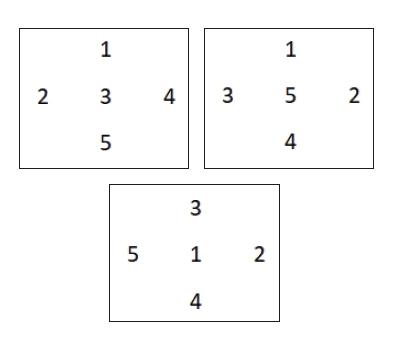
There’s no solution with 2 or 4 as the middle number. Why not?
The challenge here is to not only identify that 2 and 4 can’t be the middle number, but also to explain why. When 2 or 4 are in the middle, the remaining numbers add up to an odd number. We can’t make two equal pairs from an odd number. The numbers at the top, bottom, left and right must therefore all add up to an even number.
We can then extend this further still, by asking the children to predict what could be the middle numbers if we were using only 2,3,4,5 and 6. In this case, only the even numbers will work in the middle.
Finally, we can apply this by giving the children much larger numbers. We don’t want them to carry out the calculations; we want them to generalise and apply what they’ve already learnt. We could therefore give them 373, 374, 375, 376, 377 and see if they can explain which numbers will work in the middle and which won’t. This activity is also a great introduction to a project on magic squares.
The mysterious envelope
Last year I had the great pleasure of attending a three-day training course delivered by Juliana Loh, a master teacher of maths from Singapore. She suggested a way of differentiating an activity by content using ‘The Mysterious Envelope.’
This strategy consists of preparing three or four envelopes with different contents. Each group of children is given an envelope, the contents of which are tailored to the teacher’s assessment of what support that group will need to complete the task, or what questions they’ll need to extend and deepen their understanding.
The idea really appealed to me, as it enables teachers to support struggling children while at the same time extending more able children in a very subtle way. Everyone has an envelope, so there’s no obvious difference between who the struggling and advanced learners are. There’s also the excitement involved in opening a mysterious envelope to see what’s inside – a clear motivator for the children.
In conclusion, there are many ways to differentiate when working with one problem. There’s no need to spend hours planning different activities and producing multiple worksheets. The differentiating comes in the questioning; in the depth of the pupils’ exploration, the support we give and our expectations in terms of outcome.
Differentiating in this way will allow all children in the class to work at the limit of their capabilities, and ensure that they’re being sufficiently challenged.
Judy Hornigold is an independent educational consultant specialising in helping children with dyscalculia, and delivers training for the British Dyslexia Association and Edge Hill University.












