Adapt and Play with Mathematical Tasks So Children Are More Willing to Rise to the Challenge

Mike Askew looks at how we can adapt tasks to make them less dry and more accessible

- by Mike Askew

A teacher recently shared this task with me:
Put the numbers 1, 2, 3, 4, 5 into the spaces A, B, C, D, E. Make A + B = B + C + D = D + E
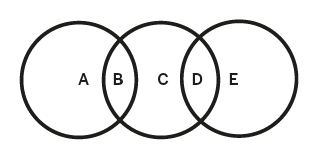
Her Y2 class, she said, had not responded well to the task, finding it difficult and giving up easily. How we can adapt tasks so that children might be more willing to ‘rise’ to the challenge? I share some thoughts here on how I would ‘play’ with this task, and others, to encourage more children to have a go.
This is an interesting challenge, but to get going on it, pupils have to process a lot of information. Claiming ‘I’m stuck’ is often, in my experience, more about not understanding what a task is asking, rather than a lack of the mathematics necessary to do it. To make this task accessible I’d get rid of the letters.
To my eye they make the task seem more complicated than it is, and are likely to put some pupils off before they start. Instead I’d present the circles in three different colours, so that each can be referred to and a language developed for describing the different sections (for example, the overlap between the red and blue circles).
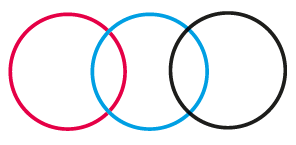
Finding the solution is likely to involve trial and improvement, so I would set it up so that, initially, no recording was involved. Instead, I’d provide digit cards to move around, or towers of interlocking cubes ranging from one to five.
I want to work on tasks that pique my curiosity and I think children are the same. As it stands, this task is rather ‘cold’ in terms of curiosity – does it matter what the solution is? To hook children in I would start with a ‘low threshold’ task.
Having made sure everyone was clear that there are five regions in the diagram I would ask them to work in pairs and put out the five number cards, one in each space. What are the totals of the cards in each circle? For example, one arrangement might be:
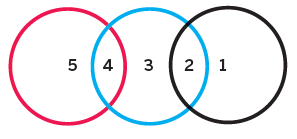
We could share some of the different totals found, with pupils rearranging the cards to see if different totals are possible. At some point, someone will produce something like:
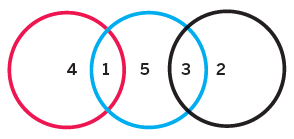
Now I could draw attention to the fact that the red circle has a total of five in it, and so does the black circle, setting up the ‘hook’. I wonder if we can arrange the numbers so that all three circles, red, blue and black, have the same total in them?
The phrase ‘I wonder’ is important for me, being more inviting than instructions like ‘make’, ‘find’ or ‘solve’. Such instructional words subtly convey the idea that there is an answer, so anyone not finding it fails.
Wondering whether or not something is possible invites pupils into a shared space of inquiry – if no solution is found, then it may not be the learner’s fault but that no solution is possible. Instructions exclude, wondering includes.
Having gone to lengths to set the task up, I want to get mileage from it. In this case, further challenges include wondering if we can still find three totals the same if we use 2, 3, 4, 5, 6, or 2, 4, 6, 8, 10, or 1, 3, 5, 7, 9. (You might like to think about why five odd numbers are going to be impossible.) I wonder what happens if we arrange the circles like this and use the digits 1 to 7?
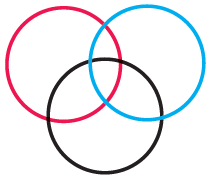
I wonder if we can do it with four circles and the digits 1 to 6?
Grid task
Let’s look at another example. A popular task is one along the lines of:
Use each of the four digits 2, 3, 5, 7 exactly once to make two two-digit numbers. Add your two numbers. What is the highest total you can find?
As a task it is OK, but it doesn’t go very far – once an answer has been found, there is not much more to do other than start over with four more digits. Let’s play with it. Again, the initial instruction is quite closed – ‘use these digits’, ‘make the largest answer’.
Starting with a two-by-two grid opens up the task. As a class, agree on four digits to use and place one in each square of the grid, for example:
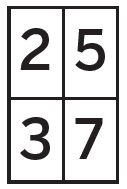
The grid can be read in two ways to create four two-digit numbers – across the rows and down the columns: 25, 37 and 23, 57. Ask pupils to add each pair and find the total of all four (or you could ask them to simply add all four straight off – a productive conversation could be had around whether there is a best order for adding them).
Ask pupils to rearrange the digits and see what happens to the overall total. Pupils will come up with different totals arising from different arrangements and now you are set up to wonder how we can arrange the digits to make the largest possible overall total.
As pupils come to find what they think is the best arrangement for this, they can be challenged to explain why that arrangement works. Is it the only one possible?
Various extensions are now possible. I wonder how to arrange the digits to make the smallest overall total? I wonder if we can arrange the digits to get as close to 200 as possible? I wonder what happens if we use four different digits? I wonder if there is a general rule for how to arrange the digits to get the greatest total?
Counting shells
A question from the 2016 KS1 reasoning paper posed:
Abdul has 9 shells. Amy has 3 more shells than Abdul. How many shells does Amy have?
So far, so closed. I would make it accessible by saying:
Abdul has some shells. Amy has more shells than Abdul. Write down a number of shells that Abdul could have and a number of shells that Amy could have. Create three pairs of numbers like this.
Besides being an accessible entry point, this would enable me to check that everyone is clear about what it means that Amy has more shells than Abdul. Having put up examples of possible pairs, I would ask pupils to work out how many more shells Amy has for each of their examples.
Next I would turn the situation around to focus on the difference:
Amy has 3 more shells than Abdul. I wonder what possible pairs of numbers there are for Abdul and Amy. Can you write down three possible pairs?
I would list some of their suggestions on the board:
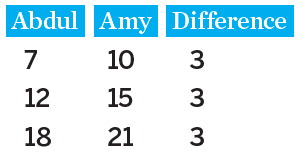
Pupils could then write the different number sentences that can be created from the numbers in each row, for example:
10 – 7 = 3; 7 + 3 = 10; 10 – 3 = 7; 3 + 7 = 10.
It would also be valuable to model each ‘triple’ on the number line.
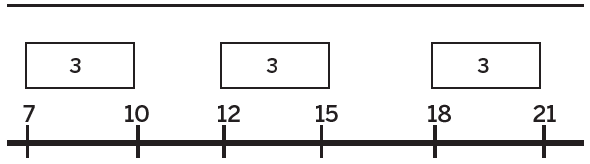
This allows for a conversation about constant difference: to keep the difference constant, what is done to one of the numbers on the line, also has to be done to its partner.
For example, if 6 was added to Abdul’s 12 to move it to 18, then 6 must also be added to Amy’s 15. Or if 5 were added to Amy’s 10 then 5 must also be added to Abdul’s 7.
Extensions include choosing a different difference between the two numbers, or one of the numbers could be given and pupils could investigate the possibilities:
Amy has 12 shells. She has more shells than Abdul. I wonder how many shells Abdul could have? What would be the difference each time?
The conversation could then focus on working systematically and looking for all solutions.
Diagonal diagrams
The KS2 2016 assessment had a question based on the diagonals of quadrilateral. A diagram like the one below was provided, with the observation that the diagonals cross at right angles:
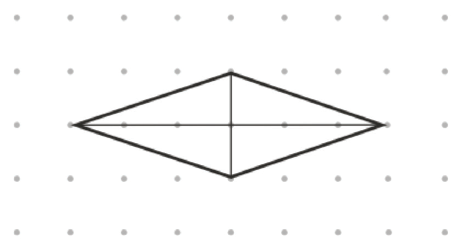
Four other quadrilaterals were given and pupils had to identify which ones had diagonals crossing at right angles. Can we open up this task?
Provide pupils with centimetre dot paper. Ask them to draw two lines that cross at right angles. The lines do not have to be of equal length, and they do not have to bisect each other (that is, the crossing point need not separate each line into two equal parts).
Share examples with the class. Did anyone draw lines that were not perpendicular to the sides of the page? If so, can they convince others that their lines do cross at right angles? For each pair of lines, pupils can join the four ends to create a quadrilateral. Ask them to name and label the quadrilaterals: square and rhombi are likely to come up.
List other types of quadrilaterals not yet found, for example, trapezium, (non-square) rectangle, (not-rhomboidal) parallelogram. Pose this challenge: I wonder if you can find if these other types of quadrilaterals will have diagonals that cross at right angles?
Extensions include creating pairs of diagonals that are the same length and creating pairs of diagonals that bisect each other (they may or may not be the same length).
Mike Askew is adjunct professor of education at Monash University, Melbourne. A former primary teacher, he now researches, speaks and writes on teaching and learning mathematics. Find him at mikeaskew.net and follow him on Twitter at @mikeaskew26.











