Number bonds – Games, worksheets and how to teach them
Help your pupils know number bonds to 20 and beyond with these lesson ideas, videos and worksheets…

- by Teachwire

If you’re a KS1 or KS2 teacher looking to teach number bonds, or refresh pupils’ memories, we’ve got all the worksheets, songs and online games you need, plus advice from top experts about how to teach this topic in creative and memorable ways.
Jump to section:
- What is a number bond?
- Number bond worksheets
- Number bond songs
- How to teach number bonds
- Number bond games
- Number bond videos
- Number bonds – the basics
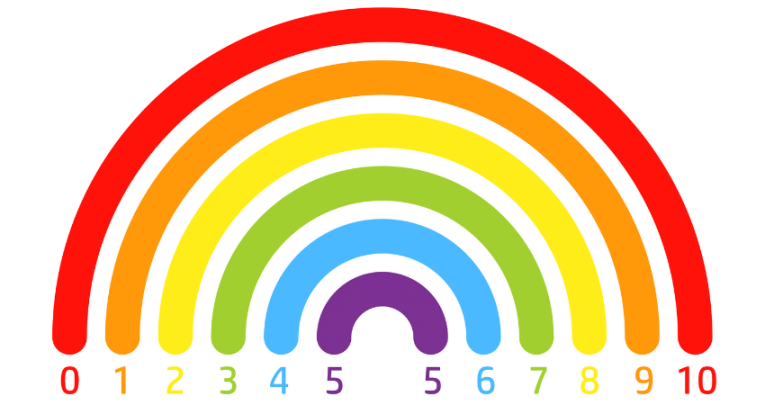
What is a number bond?
Number bonds are pairs of numbers that make up a given number. As such, they are also known as ‘number pairs’.
Number bonds worksheets
Looking for printable number bonds worksheets to use in your classroom? We’ve got you sorted.
Number bonds to 10 worksheet

Help pupils practise with our exclusive number bonds to 10 worksheet pack.
Featuring themes ranging from animals to holidays and aliens to sport, inside your free download you’ll find colourful classroom posters, card pairs and lots of illustrated worksheets for pupils to complete.

Add addition and subtraction into the mix with this number bonds to 10 worksheet pack, perfect for KS1. It’s a four-page illustrated PDF containing 12 maths problems designed to help pupils practise number bonds to 10.
Number bonds to 20 worksheet

Help KS1 pupils practise number bonds to 20 with this number bonds to 20 worksheet pack.
It has been created to match the small steps on the White Rose maths schemes of work and features a range of pictorial examples to help pupils and provoke deeper thinking.
Number bonds songs
Videos are a great way to introduce pupils to concept of number bonds – beware though, these catchy numbers will get stuck in your head for days.
Number bonds to 5 song
Number bonds to 10 song
Here’s another video with our lovely friend Jack – this time it’s the Jack Hartmaan number bonds to 10 song.
If a sedate rendition of Row, Row, Row Your Boat is more your cup of tea, here’s Mrs Simm’s Year 1 class telling you all you need to know about number bonds to 10:
Here are those lyrics in full, so your class can have a go:
9 and 1 are number bonds,
8 and 2 are friends,
7 and 3, 6 and 4,
5 and 5 are twins.
Number bonds to 20 song
How to teach number bonds
According to Jemma Sherwood, head of mathematics at Haybridge High School and Sixth Form:
“The best number sense is achieved when students know maths facts like number bonds […] by heart, because they can then work with that knowledge – which is a whole lot easier than working without it.”
The national curriculum states that by the end of Y2, KS1 pupils should “know the number bonds to 20 and be precise in using and understanding place value. An emphasis on practice at this early stage will aid fluency”.
Here we have a range of ways to help pupils to memorise and reason with number bonds to 10 and 20.
Using peppermint creams to teach number bonds in KS1
This lesson idea from Mike Askew, adjunct professor of education at Monash University, aims to teach KS1 children to collaborate, explore number facts and work systematically.
Pre-lesson preparation
Before the lesson, prepare a number of papers which the children will later use to record their results. These show arrays of squares, two by five, which are big enough to draw a simple ‘peppermint cream’ in.
You should be able to fit six arrays on a sheet of A4, but cut these up so they are all on separate slips.
Begin the lesson
Talk about the boxes of sweets you made for friends over the school break. Having a few peppermint creams for children to taste will also cause them to sit up and take notice!
“Every year I make boxes of peppermint creams for family and friends at Christmas. Who has made or tasted peppermint creams?”
Discuss these, and other sweets that the children like. Then hold up the blank array you’ve made and say:
“I always pack my peppermint creams in a box like this. Turn to the person next to you. Agree with that person how many creams I can put in a box.”
Ask children to explain how they know there are spaces for 10 creams without counting them all.
Who saw 5 + 5? Who saw 5 lots of 2?
Next, say:
I make the peppermint creams in two colours. Some are white and some are green. I put some white and some green in each box. Talk to your partner, decide on a box of creams to make and how many white and how many green creams would be in the box.”
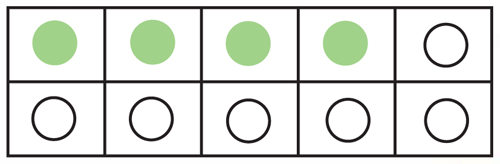
Taking some suggestions from the children, choose one example – say, 4 green and 6 white.
Invite children to help you decide where to put the creams in the box, recording this on an array as you go. Say:
“Turn to your partner. How can you be sure that there are 4 green and 6 white creams?”
While the children are checking that you’ve made the box up correctly, record a different arrangement of the 4/6 split, for example:
or
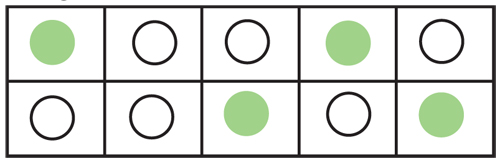
Show the children this second arrangement and ask partners to talk about whether or not this is a different box.
Deliberately leave the question vague here – in one sense, it’s different in that the creams are arranged differently. In another sense, it’s not different in that there are still 6 white and 4 green peppermints.
Continuing the lesson
Steer the children round to the idea that, for this lesson, you are going to think of these as the same box of creams. Boxes are only going to be different if the numbers of green and white creams are different. Say this:
“I was wondering – if I put a different number of green and white creams in each box, how many different boxes can I make? This is the problem I would like you to help me solve. I’d like to make as many different boxes of two types of peppermint creams as I can.”
Invite pairs to re-explain the problem to each other, and check back that everyone is clear, then say:
“You are going to work together to record the different boxes of creams and take it in turns. Here’s how – one person will be the recorder, and the other person the chooser. The chooser will say how many of each type of cream to put in the box, and the recorder will quickly draw the numbers of each type. Then you swap over.”
Invite a child to be your partner and model the way of working.
Paired activity 1
As the children settle down to work in pairs, concentrate on their taking turns appropriately and listening to each other’s instructions.
Don’t let this part of the lesson run too long – once the pairs have generated six or so boxes, direct their attention back to the board as a whole class.
Back to the problem
With everyone back together, go round the groups and ask them for one of their boxes.
Put this up on the board using Blu-Tack. Once every pair has offered up a box, ask the class if they think you have them all or if any pair has another box that we have not yet got.
More are usually offered, and inevitably you end up with some boxes that look different but actually contain the same number of each cream.
If that doesn’t happen, ‘engineer’ it by picking out and displaying some duplicates.
With a good number of boxes now on display, ask the children to have a close look and check if the ones you’ve got are all different.
Once they start to notice that there are some duplicates, ask them to talk to their partner about how you could organise the boxes so that you can see if there are any duplicates and any missing.
Working with their suggestions, order the boxes 1,9; 2,8; 3,7 and so forth.
Duplicates can be placed above each other and spaces left for any missing combinations.
Set the children back off in their pairs to continue and try and make a complete set of boxes.
Paired activity 2
Returning to the problem, the children will be more organised in checking for duplicates and missing combinations.
As they get close to creating a complete set of boxes, provide them with sugar paper and glue sticks so that they can make a poster of their set in a ‘tidy’ way.
(Most will find 9 solutions, though there are 11 in total if you allow boxes that are all-green or all-white).
Review and reflect
Gathering the children back together, choose one or more pairs to show their poster and talk about how they organised their boxes. What patterns can the children see?
Finally, work on recording the combinations using appropriate numerals and symbols.
Display the posters in class to provide reference points to pairs of numbers that make 10.
Extension activities
- What happens with three types of creams – white, pink and green. How about four types?
- What if you make boxes of 20?
- Suppose the boxes do not have to be 2 x 5, and that 12 creams could be packed in a 2 x 6 box. What other shapes of boxes would hold 12 creams? What about 24 creams?
- A box can have more than one layer. What boxes can hold 12 creams?
- White creams cost 1p and green creams cost 2p. How much does each of the boxes cost? If you have 20p to spend, what different combinations of green and white creams can you buy?
Using a kangaroo puppet to teach number bonds in KS1
Use this lesson from freelance maths consultant Chris Ingram to help your KS1 pupils explore number facts and develop their problem-solving skills.
Introducing the problem
Prepare a string of beads and hide it in the pouch of a kangaroo puppet. Say this:
“Today the kangaroo has hidden a string of beads in her pouch. There are 10 beads on the string. Some are red and some are yellow. I wonder if there are more red beads or more yellow beads? Can you draw a picture or make a number sentence to show how many of the beads could be red and how many could be yellow?”
At this point, show children the large box of beads being used and clarify:
“Can I use blue beads? Why not? Can I have 14 beads on my string? Can all 10 be yellow?”
Make sure children are clear they’re going to create a string of 10 beads, and that they must use both red and yellow beads.
Solving the problem
Differentiation is quite straightforward, and determined by whether it is more appropriate for the child to explore and record the problem practically, pictorially or symbolically.
In addition, you will probably have some children from whom a single solution is required, whereas other children will be trying to find several or even all possible solutions.
Group 1
Using the same resources as you, ask children to come up with a solution that meets the criteria – a string of 10 beads, some of which are red, some of which are yellow.
This may sound easy, but watching the children in action reveals this is more than a simple counting activity.
Most young children don’t know the number pairs that make 10, so they randomly place red and yellow beads on the string.
Some children keep count of the total as they add each bead, but most seem to put beads on until it looks as though they’ve assembled 10 – at which point they will count them to find out.
If they find there are 8 or 11 beads, hopefully they will recognise they have not enough/too many and adjust accordingly.
However, there will be many children whose response to this situation is to take all the beads off and start again, and again, and again.
This is a useful assessment point and some careful questioning here can lead children in the right direction.
Group 2
Other children might also solve the problem using different manipulatives. Explain that there aren’t enough beads to go round, and invite pupils to use something else instead.
Recognising it’s possible to represent the beads with a different item (cubes, counters, coloured bears etc) and that this won’t affect their ability to understand and solve the problem is a big step forward.
Group 3
Similarly, other groups may represent a solution pictorially using paint, crayon or coloured paper.
This requires a more sophisticated process since children are less likely to use the trial and error approach that Group 1 do (possibly because there will be ‘evidence’ of each attempt) and much more likely to use ‘counting on’ as a way of keeping track of the total as they work.
Group 4
You may have a group of higher attaining children who are able to present their solutions as number sentences.
If this is the case, they could be challenged to find all possible solutions. It will be interesting to notice whether the children work systematically in compiling an ordered list – and if they are confident they’ve discovered all the possibilities with no repeats!
Back to the problem
Once children have created their solution (whether this be with beads, paint etc), it is important to encourage them to relate this back to the original problem. Ask:
“So how many yellow beads do you think the kangaroo has, and how many red beads, and how many beads altogether?”
If it is appropriate, you might ask:
“Could we use numbers to help us remember your idea?”
Children might suggest writing the digits in yellow and red crayon or possibly creating a number sentence.
Review and reflect
Gathering the children back together after they have explored the problem is a crucial part of the process.
This is the opportunity for the kangaroo to remind the children of the original problem and for pupils to present the various solutions they have come up with.
At this point, pupils may think there are as many solutions as there are children in the class. It is your role to help the pupils to make sense of this information. Choose a child to share their solution and say something along these lines:
“Jake has made a string of beads with 3 yellow and 7 red. Does anyone have a painting or a number sentence that goes with 3 yellow and 7 red?”
Put all the presentations featuring this combination together and then move on to look at another solution.
At this stage, you will have to deal with the commutativity issue – whilst 3 + 7 is clearly equivalent to 7 + 3, you need to pay attention to the context and be careful with your use of language:

is equal to and the same as

Whichever way round you look at it, there is a group of 10 made up of 3 yellow and 7 red.

is equal to but not the same as

Or, having 3 cats and 7 dogs is not the same as having 3 dogs and 7 cats – although either way you clearly have 10 pets.
Seeing a pattern
As you collect the various solutions, begin to list them in order to encourage children to realise that, by organising the solutions in this way, you may be able to see a pattern emerging:

The pattern gives you confidence to know whether you’ve found all possible solutions and to identify any missing solutions or repeats.
Some children are more likely to see the pattern in the coloured spots, others will find the pattern clearer to see when presented using number.
Saying the pattern aloud in a chanting fashion will also help children to pick up on it.
Reorganising the beads to represent two distinct groups will make it easier to subitise or count and will help later in the session with pattern spotting.
Providing practical resources for number sentence making encourages children to experiment with symbolic recording as another way of communicating their ideas.
What’s in the pouch?
The finale to this lesson is the kangaroo revealing the beads she has in her pouch and the children identifying whether they have a solution that matches.
At this point it is important to emphasise there were nine correct solutions to the problem, not one.
Tomorrow, and maybe for the rest of the week, kangaroo can hide another 10 beads in her pouch – some red, some yellow – and the children can use their other solutions to guess what they might be.
If you display the solutions and revisit the activity regularly as a mental/oral starter, children will soon be able to use their knowledge to solve missing number problems:
“The kangaroo has 10 beads in her pouch, some are red and the rest are yellow. She will give you a clue – she will show you all the red beads, can you work out how many yellow beads there are? How do you know?”
Later you might go on to show the children how this relates to equations such as 3 + [ ] = 10 or 10 – 3 = [ ].
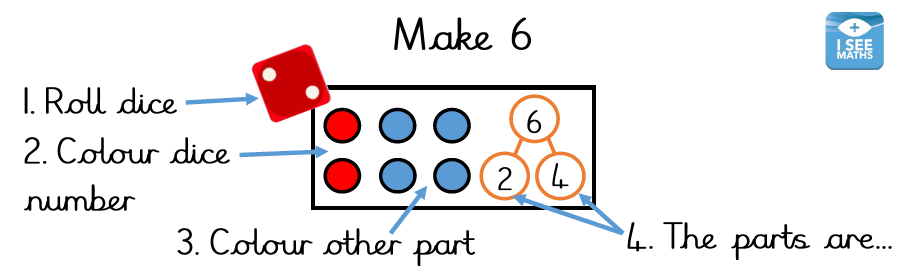
Number bonds from 6-10 dice games for KS1/2
For this simple activity you will need a dice and some colouring pencils, plus these free number bonds dice games worksheets. Here’s how to play:
- Roll a dice
- Colour in the number of circles on the dice
- Colour in the other part
- Write down the two parts that whole number is broken into
Clear the deck game
The aim of this activity, by independent educational consultant Judy Hornigold, is to help pupils develop instant recall of number bonds to ten.
Try it as a warm-up activity at the start of a lesson, or at the end for revision or consolidation.
How to play
You will need four sets of digit cards from 1 to 9. Shuffle the cards and place them face up on the table in three rows of four. Players take it in turns to pick up pairs of cards that add up to 10.
The gaps that are left are then filled with cards from the remaining pack. The idea is to take it in turns and spot the pairs that make 10 as quickly as possible.
More ideas for how to teacher number bonds
Don’t mind running the risk of a thoroughly good soaking from Freddie in Y1? Give this one a go…
This idea from Miss Ward involves a little pre-preparation but focuses on the ultimate number bonds to 10 tool – our own fingers…
You’ll only need a cup and some two-sided counters to recreate this simple game from Mrs Baillie…
Number bond games
Teaching number bonds to 10 can sometimes feel a little samey. After all, there are only a small number of combinations. So why not let kids do something fun to either learn, or consolidate their learning of, number facts?
Here are a selection of free, easy-to-use online number bond games for your class to try out.
Number bonds to 10 games
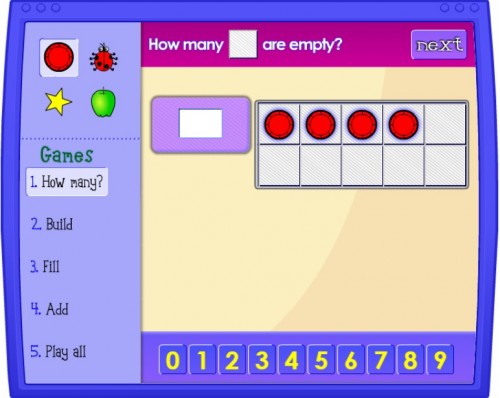
This simple but handy ten frame number bonds game features a grid of 10 spaces which it fills with counters (or stars, apples or ladybirds) and asks either how many there are, or how many spaces are empty.
You can also advance onto the ‘build’ level where children have to insert the correct number of counters. Then there’s ‘fill’, where they are asked how many more counters are needed to complete the set of 10. And ‘add’ where you have two sets of 10 to fill with the correct number of counters, before adding the totals together.

Learn number bonds to 10 with this Curious George: Museum of Tens number bonds game.
Follow him around the museum where each exhibit should have 10 items, but some are missing. It’s your pupils’ job to help George work out how many more they need to make up 10.

In this fun little Dress Your Monster number bonds game, children get to dress their monster with various clothes and accessories.
But in order to do so they’ll need to answer number bonds questions up to 10.

A line of numbered balls is rolling its way towards a hole in this number bonds to 10 game, and your job is to stop it. You do this by firing your own spheres to make number bonds of 10 and watch them disappear. It’s brilliantly addictive.
Timed games
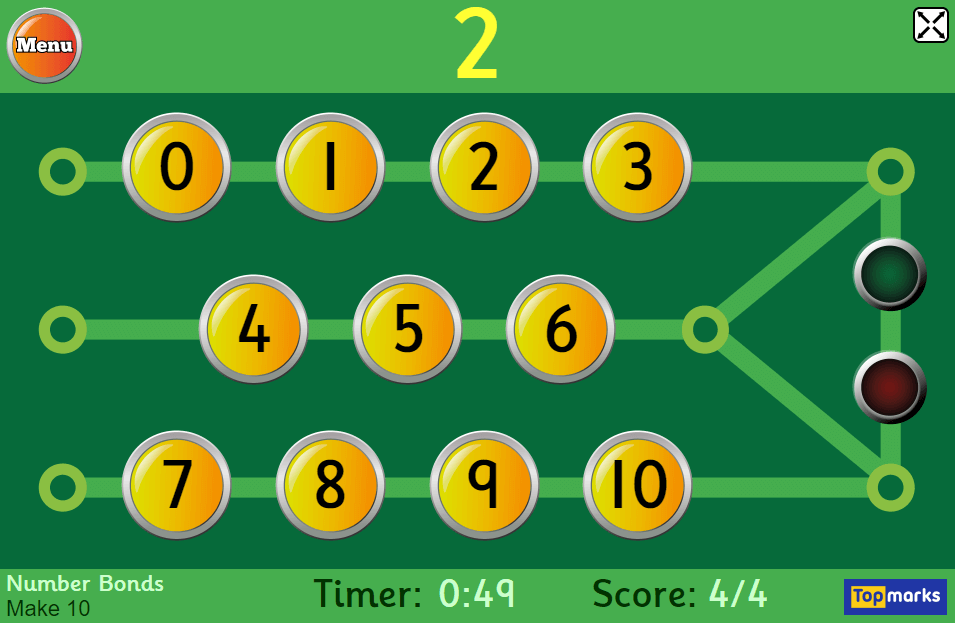
This quickfire Hit the Button number bonds game has a number of options for you to try including doubles, halves, times tables, division facts and square numbers, plus, of course, number bonds.
Even within number bonds you can select number bonds up to 10, 20 or 100, and then there are different challenges within those still.
With the basic number bonds to 10, children are given one number, and have to select the number that will pair up to make 10. They have a minute to get as many as possible.
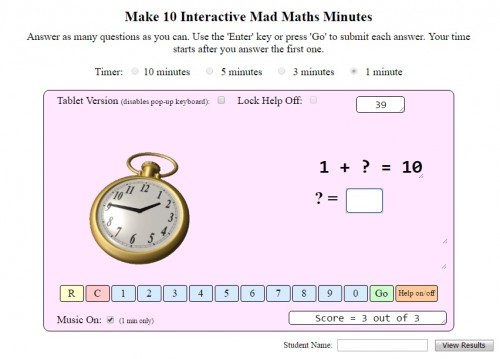
An even simpler version is this Mad Maths Minute number bonds game (although you can set a longer timer if you like) where children need to answer as many number bonds to 10 sums as possible in 60 seconds.
There’s a help option which gives you a coloured 10 frame to offer visual aid, and you can check and print out your results too.

Another variant on the beat-the-clock system, this I Can Recall All Number Bonds to 10 game has the benefit of subtraction questions being thrown into the mix.
Get consecutive questions correct to boost your level, but beware, that makes the sums increase in difficulty.
Advanced game

This number bonds game is one of those fun little puzzle games that you could play for hours.
The idea is to connect number bonds to 10 by clearing a path between them. Your line can bend once, twice or the balls can be next to each other (not diagonally). Just remember to keep an eye on how long you’ve been playing!
Browse more maths games KS1 ideas and maths games KS2 ideas.
Number bond videos
We’ve rounded up some of the best video guides on the web to give you a few simple ideas how to teach your Key Stage 1 pupils their number bonds to 10.
1 | A Guide to Number Bonds
This simple guide from Komodomath might help you focus on how you present number bonds to your class, and there’s also a video for subtracting with number bonds and teaching them in the Singapore style.
2 | Singapore Maths
Talking of which, here’s Mr Almeida with an animated guide on doing things the Singapore way.
3 | Maths at Home
Or, if you don’t want to travel quite so far, or anywhere at all for that matter, this video from Maths@Home shows you how to use everyday household (or classroom) items to help children get a tangible grasp on number bonds.
4 | CBeebies Tower Blocks
One fun challenge from CBeebies is to get children to try to build a number block tower, finding different ways to make 10 without their structure collapsing.
5 | Wish Fish
Another fun way to let children learn is to play a Matching Pairs-style game with Wish Fish.
6 | Interactive lesson plans and teaching resources
Want something a bit more hi-tech? IWBs are great visualisers for teaching number bonds, as Promethean Planet shows here.
7 | Getting to 10 by Filling in Boxes
And this method devised by Khan Academy just seems too simple pass up. It’s a brilliantly basic way of helping children understand number bonds through getting to 10 by filling boxes.
Number bonds – the basics
Looking for a refresher on the concept of number bonds? Here’s what you need to know, in a nutshell.
To 5
Number bonds to 5 are pairs of numbers that add together to make 5. Number bonds for the number 5 are:
- 0 + 5
- 1 + 4
- 2 + 3
- 3 + 2
- 4 + 1
- 5 + 0
To 10
Number bonds to 10 are pairs of numbers that add together to make 10. Number bonds for the number 10 are:
- 0 + 10
- 1 + 9
- 2 + 8
- 3 + 7
- 4 + 6
- 5 + 5
- 6 + 4
- 7 + 3
- 8 + 2
- 9 + 1
- 10 + 0
To 20
Number bonds to 20 are pairs of numbers that add together to make 20. The number bonds to 20 are:
- 0 + 20
- 1 + 19
- 2 + 18
- 3 + 17
- 4 + 16
- 5 + 15
- 6 + 14
- 7 + 13
- 8 + 12
- 9 + 11
- 10 + 10
- 11 + 9
- 12 + 8
- 13 + 7
- 14 + 6
- 15 + 5
- 16 + 4
- 17 + 3
- 18 + 2
- 19 + 1
- 20 + 0
Number bonds to 100
Number bonds to 100 are pairs of numbers that add together to make 100. Here’s a list of number bonds to 100, if working in multiples of 10:
- 0 + 100
- 10 + 90
- 20 + 80
- 30 + 70
- 40 + 60
- 50 + 50
- 60 + 40
- 70 + 30
- 80 + 20
- 90 + 10
- 100 + 0











